ご冗談でしょう?名無しさん2017/02/27(月) 18:51:45.68 ID:??? それでは問題 今、列車の中央にいる乗客が、ある電柱の横を通り過ぎるときに自分の時計と電柱の時計を見比べたら、どちらもちょうど0秒をさしていた。 そして列車の速度は0.86cなのに電柱の間隔はその半分しかないので、乗客は自分の時計で0.5秒後に次の電柱の脇を通り過ぎるのを見ることになる。 一方、電柱の脇に立っている人から見ても、最初の電柱の脇を列車の中央にいる乗客が通り過ぎるときにどちらの時計もちょうど0秒をさしているのを見る。 列車の速度は0.86cであるから、この乗客が次の電柱の横を通り過ぎるのはちょうど1秒後である。 このとき、列車の乗客の時計は0.5秒をさしていて、その横の電柱の時計は1秒をさしている。 電柱の時計は全て合わせてあるから、最初の電柱の時計もちょうど1秒をさしている。 従って、列車の乗客から見ても、乗客の時計は0.5秒を指していて、電柱の時計は1秒をさしていることになる。 すなわち、どちらの系から見ても、列車の乗客の時計は線路の系の時計の半分の速度で動いているということになる。 これは運動は相対性であるという相対性理論に反するのではないか? 196 : ご冗談でしょう?名無しさん2017/02/28(火) 08:10:56.02 ID:??? では、論理的に。 前提。 電柱の脇を0.86cで走る列車を、電柱と列車の双方の視点で見ると、 互いの時刻は半分に遅れて見える。 長さが半分に縮むように見える。 条件。 列車の中央にいる乗客が、ある電柱の横を通りすぎた瞬間、 乗客、電柱、双方の時計は0時となっていた。 で、 >列車の速度は0.86cであるから、この乗客が次の電柱の横を通り過ぎるのはちょうど1秒後である。 >このとき、列車の乗客の時計は0.5秒をさしていて、その横の電柱の時計は1秒をさしている。 >電柱の時計は全て合わせてあるから、最初の電柱の時計もちょうど1秒をさしている。 >従って、列車の乗客から見ても、乗客の時計は0.5秒を指していて、電柱の時計は1秒をさしていることになる。 >すなわち、どちらの系から見ても、列車の乗客の時計は線路の系の時計の半分の速度で動いているということになる。 上記の説明は前提に反するので、この説明はウソである。 : ご冗談でしょう?名無しさん2017/02/28(火) 08:47:11.33 ID:??? ちなみに、このときも次のように続けることができる。 今、列車の中央にいる乗客が、ある電柱の横を通り過ぎるときに自分の時計と電柱の時計を見比べたら、乗客の時計は0.5秒をさし、電柱の時計は1秒をさしていた。 >そして列車の速度は0.86cなのに電柱の間隔はその半分しかないので、乗客は自分の時計で0.5秒後に次の電柱の脇を通り過ぎるのを見ることになる。 >一方、電柱の脇に立っている人から見ても、最初の電柱の脇を列車の中央にいる乗客が通り過ぎるときにどちらの時計もちょうど0秒をさしているのを見る。 >列車の速度は0.86cであるから、この乗客が次の電柱の横を通り過ぎるのはちょうど1秒後である。 このとき、列車の乗客の時計は1秒をさしていて、その横の電柱の時計は2秒をさしている。 >電柱の時計は全て合わせてあるから、最初の電柱の時計もちょうど2秒をさしている。 従って、列車の乗客から見ても、乗客の時計は1秒を指していて、電柱の時計は2秒をさしていることになる。 このようにして列車が次々と電柱の横をとおりすぎるとき、乗客の時計は電柱の時計の半分の値を示すことになる。 すなわち、電柱(線路)の静止系に対して乗客の時計は常に半分の速度で進む。 215 : NAS6 ◆n3AmnVhjwc 2017/02/28(火) 10:28:07.06 ID:fC90M1kr その上でお前らの話に敢えて合わせるとしたら 今、列車の中央にいる乗客が、ある電柱の横を通り過ぎるときに自分の時計と電柱の時計を見比べたら、どちらもちょうど0秒をさしていた。 そして、電柱の速度は-0.86cだから、電柱の間隔はその半分しかないので、乗客は自分の時計で0.5秒後に次の電柱の脇を通り過ぎるのを見ることになる。 しかしこの時の電柱の時計は0.25秒後である 一方、電柱の脇に立っている人から見ても、最初の電柱の脇を列車の中央にいる乗客が通り過ぎるときにどちらの時計もちょうど0秒をさしているのを見る。 列車の速度は0.86cであるから、この乗客が次の電柱の横を通り過ぎるのはちょうど1秒後である。 このとき、列車の乗客の時計は0.5秒をさしていて、その横の電柱の時計は1秒をさしている。 電柱の時計は全て合わせてあるから、最初の電柱の時計もちょうど1秒をさしている。 従って、お互いの時計は相手の時計が半分の速度で動いているということになる。 234 : ご冗談でしょう?名無しさん2017/02/28(火) 12:59:18.52 ID:??? >>230 >しかしこの時の電柱の時計は0.25秒後である 間違い。 やっぱり偉そうに書いてても茄子はわかってなかったか。 いいか?線路の横の人から見たら、乗客の時計は0.5秒をさしていて、電柱の時計は1秒をさしているんだよな? これは認めてたよな? すると、2つの時計の距離がほぼゼロとすると、 ローレンツ変換の式で、距離がほぼゼロだからこの2つの時計の事象は誰から見ても同時だ。 すなわち誰から見ても、乗客の時計は0.5秒をさしていて、電柱の時計は1秒をさしていることになる。 だから乗客から見ても、電柱の時計は1秒をさしている。 247 : ご冗談でしょう?名無しさん2017/02/28(火) 13:35:54.64 ID:??? >>242 >自分の系はともかく、相手の系の自分の系からの見え方は目の錯覚なだけだから 錯覚なんかじゃない。 例えば列車の乗客は0.5秒ごとに点滅するライトを持っていて、 電柱には1秒ごとに点滅するタイトが付いているとする。 最初の電柱を通り過ぎるときにちょうど両方のライトが点灯したとする。 そして線路の静止系瀬見たとき、 乗客のライトは0.5秒たったので点灯している。 電柱のライトは1秒たったので点灯している。 このフタチの事象は同じ場所で起こったので、どの座標系から見ても同時に点灯したのを見ることになる。 従って乗客から見ても、電柱のライトは1秒後の点灯をしたところであり、2つのライトが同時に点灯したのを見ることになる。 ところが茄子のりろんだと、このとき電柱では0.25秒しかたっていないから電柱にはライトが点灯していない、すなわち乗客のライトしか点灯していないことになる。 乗客から見たら乗客のライトしか点灯しておらず、それ以外の人から見たら2つのライトが同時に点灯しているというのは矛盾だ。 つまり茄子の理論は間違っているということだ。 277 : NAS6 ◆n3AmnVhjwc 2017/02/28(火) 15:18:41.00 ID:fC90M1kr もうちょい分かりやすくすると 二つの運動物体の、例えば0秒から1秒になる瞬間は必ずしも同時の瞬間じゃない っていう同時刻の相対性ってことだろ 278 : ご冗談でしょう?名無しさん2017/02/28(火) 15:24:01.01 ID:??? >>275 だから、何度も書いたし、お前自身も確認したように、 同時刻の相対性で2つの事象が起きた時刻が観測する系によって異なるのは、 2つの事象が離れた場所にある時だけ。 ローレンツ変換の、同時刻の相対性で2つの事象の起きる時刻がどれだけずれるかを計算する式をよく確認しろ。 その式によればずれる時刻は2つの距離(及び速度)に依存するだろ。 逆に言えば、2つの事象の距離がゼロの時はどの系から見ても2つの事象が起きた時刻は同じになるわけだ。 ちなみに、今回の問題は、前に茄子には、なぜGPSの時計の補正は地球上より衛星の時計が遅れるとして補正するのかでの説明と同じ理屈だ。 280 : ご冗談でしょう?名無しさん2017/02/28(火) 15:25:17.68 ID:??? >>277 だからお前は「同時刻の相対性」がちっともわかってない、っていうか、同時刻の相対性を求める式の意味がわかってないということだ。 >>278をよく読め。 282 : ご冗談でしょう?名無しさん2017/02/28(火) 15:35:11.85 ID:??? >>279 お前の得意な時空図ばどうした? それで、どの座標系から見ても光速は同じ角度なのはどうしてだと思う? どの座標系から見ても光速は一定だからだ。 例えば時空図のある一点に列車の先端があったとすると、その先端がいる場所とその時の時刻は誰が見ても同じ。 だけど、その時、同時に後端がいる時刻と場所は同時刻の相対性により観測する系ごとに異なる。 これこそが列車の長さが異なって見える理由だ。 列車の先端と後端で同時にランプが点灯したとする。 だが、観測する系によっては先端のランプが先に点灯して後端のランプが後から点灯したように見える系もあれば、逆に後端のランプが先に点灯して先端のランプが後から点灯するように見える系もある だが列車の中央で2つのランプが同時に点灯したとすると、これはどの系から見ても同時なんだよ 295 : ご冗談でしょう?名無しさん2017/02/28(火) 16:16:12.70 ID:??? >>293 「わけわかんないけど、相対性理論はそうなっているということでFA」 ということでいいんだな? 地上から見たら列車の乗客が電柱の横を通ってから次の電柱の横に来るまでちょうど1秒かかる だからその時の電柱の時計は1秒をさしている この時列車の中の時間の進みは半分になったように見える。従って乗客の持っている時計は0.5秒をさしている これは認めているにもかかわらず 一方、乗客から見たら、電柱の間隔が半分になっているから最初の電柱の横を通ってから次の電柱の横に来るまで0,5秒しかたっていない。それゆえ、次の電柱の横に来た時乗客の時計は0.5秒をさしている。 ここまではいい。 問題はその時、電柱の時計が何秒をさしているかということ。 乗客は外の時計の進みは自分の時計の進みの半分になっていると思うはず。 なのに電柱の時計は1秒をさしている。 それはなぜか? もう何度も質問している。 一向にまともな答えが返ってこない。 結局、茄子はちゃんと理解していないということだ。 そろそろ降参か? 322 : ご冗談でしょう?名無しさん2017/02/28(火) 17:46:54.98 ID:??? 列車の中央から光を出したら、列車の前後に同時に届く そこで光が届いた時に列車の前後の時計を0秒に合わせる これで列車の静止系(以後列車の系)では前後の時計が合ったことになる ここで、地上の静止系(以後地上の系)から見たら、光は先に後端に到達するから、まず後ろの時計が0秒に合わせられ、しばらくたってから光が先端に到達して前方の時計が0秒に合わせられたことになる。 従って列車の時計を見ると先端の時計より後端の時計の方が進んだ時刻をさしている。 さて、いま列車の系で見ると、電柱の間隔は半分になっているから、列車の先端がある電柱の横を通り過ぎた瞬間には、後端はちょうど電柱2本分だけ後ろの電柱の横を通り過ぎようとしているところだ。 この時当然先端の時計も後端の時計も同じ時刻をさしている。例えばこの時の秒針がちょうど0秒をさしていたとする。 一方地上の系から見たら先端がある電柱の横を通り過ぎるときやはり先端の時計はちょうど0秒をさしている。 ところが地上の系から見ると、列車の後端の時計は0秒よりも進んだ時刻をさしている。 それゆえ列車の中で0秒をさしていた時に通り過ぎた電柱の位置より少し進んだ位置にあることになる。 こうして地上から見ると、列車の前後の時計の指す時刻が異なるために、先端と後端がそれぞれの時計がしました時刻にどこにいるかに従った場所にいることになるため長さが縮むことになる これがローレンツ短縮で列車が縮む理由だ。 ここまではいいかな? 325 : NAS6 ◆n3AmnVhjwc 2017/02/28(火) 17:56:58.40 ID:fC90M1kr >>322 これも言えるね ここで、列車の系から見たら、光は先に先端の電柱に到達するから、まず前の時計が0秒に合わせられ、しばらくたってから光が後端の電柱に到達して後ろの時計が0秒に合わせられたことになる。 従って電柱の時計を見ると後端の電柱の時計より先端の電柱の時計の方が進んだ時刻をさしている。 328 : ご冗談でしょう?名無しさん2017/02/28(火) 18:05:28.40 ID:??? >>325 素晴らしい。 そこに気づいたか。 その通り、時計は乗客と最初の電柱だけでなく、全ての電柱についている。 そして地上の系で全ての電柱の時計が合わせてある。 しかし列車から見ると電柱の時計の指し示す時刻は全て異なっているんだ。 ある電柱にランプをつけて、その前後の電柱に向けて光を発したら、地上の系では両方の電柱に同時に光が届く。 でも列車から見たら、先端の方の時計に先に光が到達し、後端の方の電柱の方が後から光が当たる。 従って電柱のそれぞれの時計は先端の先の方の電柱ほど進んだ時刻ををさしていることになる。 330 : ご冗談でしょう?名無しさん2017/02/28(火) 18:12:28.86 ID:??? ここまで来たらもうわかったろう。 まず乗客は最初の電柱の横を通った時、電柱の時計も自分の時計もちょうど0秒をさしていることを見る。 これはどの系から見ても同じように見える。 次に乗客は今通り過ぎた電柱についている時計の進む速度が自分の時計の進む速度のちょうど半分しかないことを見る。 そして次の電柱の横を通り過ぎるとき、その電柱の時計は最初の電柱の時計より進んだ時刻をさしている。その結果、乗客は自分の時計はまだ0.5秒をさしているのに電柱の時計はちょうど1秒をさしているのを見る。 だけど、最初に通り過ぎた十名はまだ0.25秒をさしているわけだ。 さらに次の電柱の横に来た時、乗客の時計はちょうど1秒をさして、その電柱の時計は2秒ちょうどをさしている。そしてさっき1秒をさしていた電柱の時計はいま1.25秒をさしているわけだ。 こうして列車から見ると地上の時計の進みは遅くなっているが次々とくる電柱の時計は2倍の速さで進んだ時刻をさしているということが起きるわけだ。 333 : NAS6 ◆n3AmnVhjwc 2017/02/28(火) 18:18:29.98 ID:fC90M1kr おっけ でさ、そうやって設定された「同時刻」の相対性ってさ、 加速中に設定されるわけ? いつ時刻がずれたのかな? 335 : NAS6 ◆n3AmnVhjwc 2017/02/28(火) 18:22:40.35 ID:fC90M1kr 「速度によって」同時刻の相対性が設定されるんだから 急加速や緩加速など加速度そのものにはよらないんだろ で、加速中に同時刻の相対性が設定されるって どうなってるん? 343 : NAS6 ◆n3AmnVhjwc 2017/02/28(火) 18:43:57.63 ID:fC90M1kr エレベーターの左から光を発射と同時に上へ加速 すると光が下に湾曲する その左からの光より下の方から光を発射したとすると 先ほどよりさらに湾曲する ゆえに低い位置ほど時計の進みが遅い これをそのまま重力場として扱う 354 : ご冗談でしょう?名無しさん2017/02/28(火) 19:13:33.16 ID:??? 地上での電柱と乗客の時計の時刻(電柱:静止、乗客:速度v→) 電柱1 電柱2 電柱3 電柱4 電柱5 0 0 0 0 0 乗客 0 電柱1 電柱2 電柱3 電柱4 電柱5 1 1 1 1 1 乗客 0.5 電柱1 電柱2 電柱3 電柱4 電柱5 2 2 2 2 2 乗客 1 電柱1 電柱2 電柱3 電柱4 電柱5 3 3 3 3 3 乗客 1.5 電柱1 電柱2 電柱3 電柱4 電柱5 4 4 4 4 4 乗客 2 355 : ご冗談でしょう?名無しさん2017/02/28(火) 19:13:46.94 ID:??? 列車での電柱と乗客の時計の時刻(乗客:静止、電柱:速度←v) 電柱1 電柱2 電柱3 電柱4 電柱5 0 0.75 1.5 2.25 3 乗客 0 電柱1 電柱2 電柱3 電柱4 電柱5 0.25 1 1.75 2.5 3.25 乗客 0.5 電柱1 電柱2 電柱3 電柱4 電柱5 0.5 1.25 2 2.75 3.5 乗客 1 電柱1 電柱2 電柱3 電柱4 電柱5 0.75 1.5 2.25 3 3.75 乗客 1.5 電柱1 電柱2 電柱3 電柱4 電柱5 1 1.75 2.5 3.25 4 乗客 2 359 : NAS6 ◆n3AmnVhjwc 2017/02/28(火) 19:30:07.50 ID:fC90M1kr 加速して、ある速度の系に乗り換えごとに、その時刻設定がなされる になってるんだけど もっとうまく説明するとどんなんだろ 361 : NAS6 ◆n3AmnVhjwc 2017/02/28(火) 19:37:34.73 ID:fC90M1kr で、 加速して、時刻設定がなされる 理由ね 加速時になんで行われるか ってことが >>343 低い位置ほど時計の進みが遅い から時刻設定されるんよ 362 : NAS6 ◆n3AmnVhjwc 2017/02/28(火) 19:44:15.80 ID:fC90M1kr 電柱1 電柱2 電柱3 電柱4 電柱5 0 0.75 1.5 2.25 3 乗客 →加速 低い位置ほど時計の進みが遅い って対応 878 : NAS6 ◆n3AmnVhjwc 2017/03/05(日) 14:57:15.22 ID:AxjzRidV イスカンダルまでの距離をlとする ヤマトの速度をvとする ヤマトの固有時間、固有長さをそれぞれT、Lとする 1/γ=√(1-(v/c)^2)とする 地球の時計では片道t=l/v 地球からヤマトの時計はT=(l/vγ)=t/γ=L/v ヤマトから見ると距離はL=l/γ 到着までの時間はT=(l/vγ)=t/γ=L/v 往復はそれぞれ倍 (1/γ)=√(1-(v/c)^2) 固有時間T=(1/γ)t 固有長さL=(1/γ)l 固有速度v=L/T=l/t で双子のパラドックスはFA 879 : NAS6 ◆n3AmnVhjwc 2017/03/05(日) 15:13:50.12 ID:AxjzRidV 衛星時間τ τ0|---------|τ1 \ 光路差\ 地上時間t |-t0|-----|t1 固有時間τ=(1/γ)(t1-t0) 衛星から時刻情報兼開始命令が来て t(-光路差)=(t1-t0)(-光路差)の期間と τ=(τ1-τ0)の期間が同時ってことだよん もう少し分かりやすく時空図を描くと ttp://nas6.net/jikuuzu2.png
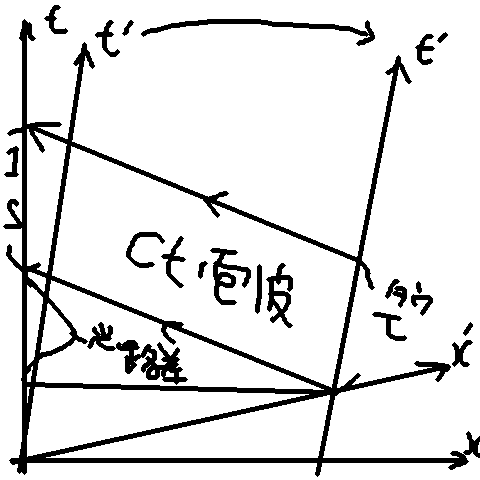
固有時間τ=(1/γ)t τとtが同時 後手五5ピンポン 同時って素晴らしい 881 : NAS6 ◆n3AmnVhjwc 2017/03/05(日) 15:17:37.60 ID:AxjzRidV で、 ttp://nas6.net/jikuuzu2.png これの 固有時間τとtがそれぞれの時間の進み方で 光路差が、同時刻の相対性のいわゆる時刻のずれなわけだ 882 : NAS6 ◆n3AmnVhjwc 2017/03/05(日) 15:24:31.38 ID:AxjzRidV >>878-881 ってスゲー分かりやすいんだけど 俺だけそう感じるのかな GPSは 光速度:c=299792458[m/s]、万有引力定数G=6.67259e-11[m^3/kgs^2]、 地球の質量mE=5.9736e+24[kg]、地球のシュバルツシルト半径rg=2GmE/c^2=7.97188e+14/c^2=8.86991e-3[m]、 GPS衛星の速度vA=4000[m/s],GPS衛星の軌道rA=2.6556752e+7[m] 地球の半径rE=6.356752e+6[m]、地球の自転速度vE=4.62276e+2[m/s],GPS衛星の高度hA=rA-rE=2.02e+7[m] GPS衛星が高度hAで周回している GPS衛星の地上から見た固有時間は τA=t(√(1-rg/rA)√(1-vA^2/c^2))/(√(1-rg/rE)√(1-vE^2/c^2)) とする 今、GPS衛星からGPS衛星時刻0の電波が地上の受信機に送られ つづいてGPS衛星時刻τA=86400.000038263[s]で再び送られたとき その状況を説明しなさい 光路差d=hA/c=0.06738[s]と求められ 地上でGPS衛星時刻0を受信した瞬間、それを発信した瞬間より 光路差d遅れている、その時の地上の時刻をt0とする 地上でGPS衛星時刻τAを受信した瞬間、それを発信した瞬間より 光路差d遅れている、その時の地上の時刻をt1とする ここでτA=86400.000038263[s]とするとt=t1-t0は、 τA=t(√(1-rg/rA)√(1-vA^2/c^2))/(√(1-rg/rE)√(1-vE^2/c^2))より t=τA(√(1-rg/rE)√(1-vE^2/c^2))/(√(1-rg/rA)√(1-vA^2/c^2)) =86400.000038263(√(1-8.86991e-3/6.356752e+6)√(1-(4.62276e+2/299792458)^2))/(√(1-8.86991e-3/2.6556752e+7)√(1-(4000/299792458)^2)) =86400.000038263((0.999999999302324)(0.9999999999988111))/((0.999999999833000)(0.999999999910988)) =86400.0[s]=1[day]と求められる GPS衛星時刻0 GPS衛星時刻τA=86400.000038263 |------------------| \ | \光路差d=0.06738 \光路差d=0.06738 |------------------| 地上で時刻0受信 地上で時刻τA受信 地上時刻0 地上時刻86400 ttp://nas6.net/jikuuzu2.png ttp://nas6.net/jikuuzu3.png

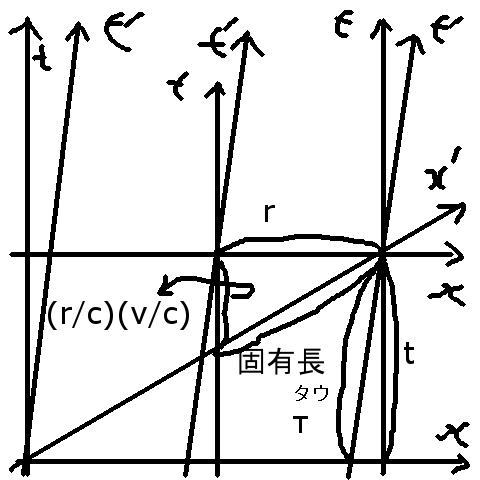
の関係 この時空図の t-x系が地上、t'-x'系がGPS衛星 ct電波が衛星時刻情報の電波 光路差が光路差d 1[s]がt=86400[s] τがτA=86400.000038263[s] 時刻のずれは(r/c)(v/c)なので 光路差がそのまま時刻のずれというのは 正確ではないけどファクターではある 長さを調べると、図の固有長、固有時は逆数というのが正確かもしれない 24 : NAS6 ◆n3AmnVhjwc 2017/03/08(水) 11:04:16.16 ID:Rf397G0y ローレンツ変換f()は |t'|=γ|1 -v/c^2||t| |r'| |-v 1 ||r| γ=1/√(1-(v/c)^2) t'=γ(t-rv/c^2) t'=γt-γrv/c^2 tについて解いて t=(1/γ)t’+rv/c^2 時間の進み方(固有時間)は(1/γ)t 固有時間からの時刻のずれは(r/c)(v/c) 34 : NAS6 ◆n3AmnVhjwc 2017/03/08(水) 13:43:52.46 ID:Rf397G0y >>24 を、もったいぶって、あんまり教えないんだよね 14 : ご冗談でしょう?名無しさん2017/03/08(水) 10:14:23.37 ID:??? 列車の長さは25.8万キロメートル。 客車は10台編成で、1両の長さは、2.58万キロメートル。 電柱の間隔は25.8万キロメートルで、 その間にも、2.58万キロメートルごとに電柱が立ってることにしよう。 列車の前部の客車が、ある電柱を通り過ぎたとき、電柱の時刻は1秒だった。 列車の前部の客車は、0.5秒だった。 そのとき、列車の後部の客車が、5本後ろの電柱を通り過ぎた。 電柱の時刻は1秒だった。 その電柱から見た列車の後部の客車の時刻は、0.5秒でいいの? 0.86cで等速で、列車が走る場合。 148 : NAS6 ◆n3AmnVhjwc 2017/03/12(日) 11:44:01.81 ID:Kls3mMIS >>146 だから >>14-15 はこうだった 固有時間は τA=0.5t、τO=0.5τA=0.25t 時刻のずれは (r/c)(v/c) 前部(0c/c)(0.86c/c)=0 中部(0.086c*5/c)(0.86c/c)=0.37 後部(0.086c*10/c)(0.86c/c)=0.74 地上からみたらt=0 地上0.00 地上0.00 地上0.00 地上0.00 地上0.00 列車0.74 列車0.37 列車0.00→ 地上からみたらt=1 地上1.00 地上1.00 地上1.00 地上1.00 地上1.00 列車1.24 列車0.87 列車0.50→ 列車からみたらt=0 地上-0.74 地上-0.37 地上0.00 地上0.37 地上0.74 列車0.00 列車0.00 列車0.00→ 列車からみたらt=1 地上-0.49 地上-0.12 地上0.25 地上0.62 地上0.99 列車0.50 列車0.50 列車0.50→ 地上からみて 地上1.00のとき 前部0.50 中部0.87 後部1.24で通過 列車からみて 地上1.00のとき 前部1-0.99+0.5=0.51 中部1-0.62+0.5=0.88 後部1-0.25+0.5=1.25で通過 146 : NAS6 ◆n3AmnVhjwc 2017/03/12(日) 11:31:04.14 ID:??? 長さ0.06cの列車10両が0.6cで走る A:列車、O:地上とすると 固有時間は τA=0.8t、τO=0.8τA=0.64t 時刻のずれは (r/c)(v/c) 前部(0c/c)(0.6c/c)=0 中部(0.06c*5/c)(0.6c/c)=0.18 後部(0.06c*10/c)(0.6c/c)=0.36 地上からみてt=0 地上0 地上0 地上0 地上0 地上0 列車0.36 列車0.18 列車0 地上からみてt=1 地上1 地上1 地上1 地上1 地上1 列車1.16 列車0.98 列車0.8 地上1で 前部0.8 中部0.98 後部1.16 列車からみてt=0 地上-0.36 地上-0.18 地上0 地上0.18 地上0.36 列車0 列車0 列車0 列車からみてt=1 地上0.28 地上0.46 地上0.64 地上0.82 地上1 列車0.8 列車0.8 列車0.8 地上1で 前部0.8 中部1-0.82+0.8=0.98 後部1-0.64+0.8=1.16