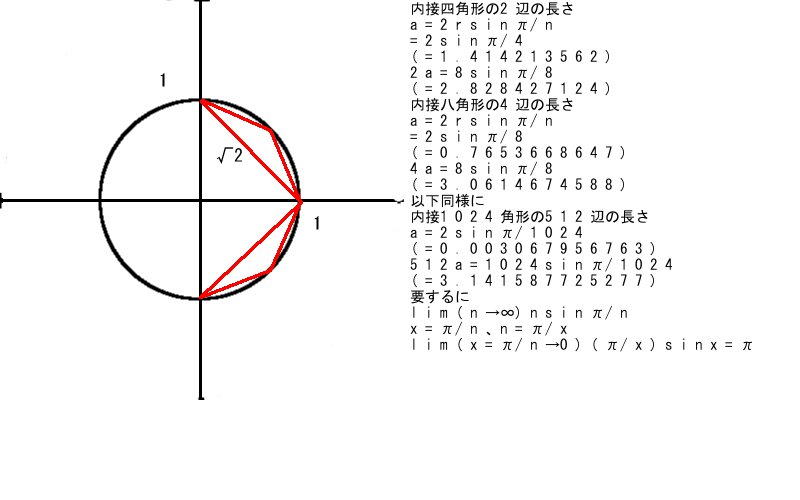
円周率
π=3.1415926535897932384626433832795
≒
√2+√3=3.1462643699419723423291350657156
と近似できる
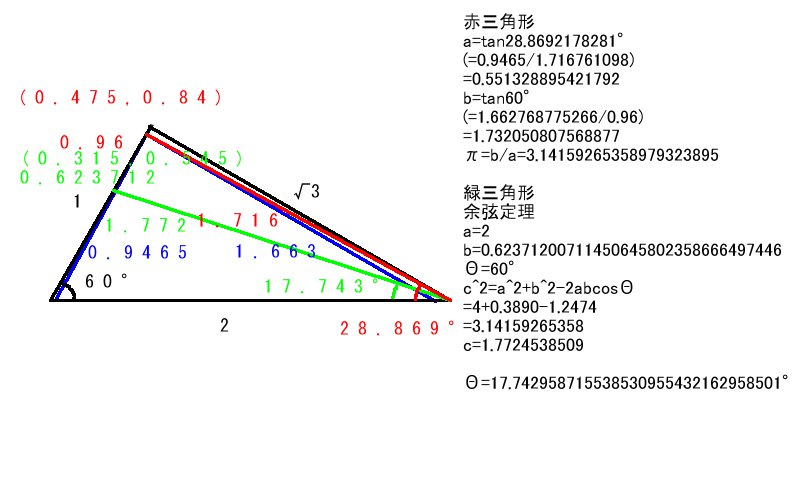
円周率三角形
√3を考えてたらこんな円周率三角形を思いついた
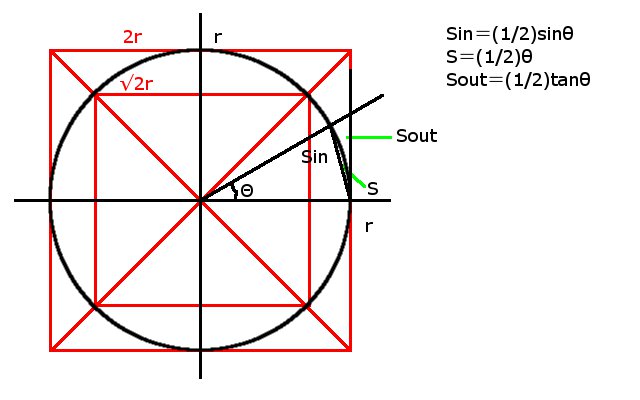
内接多角形の面積
Sin=(1/2)sinθ、S=(1/2)θ、Sout=(1/2)tanθ
となり、ここで θ=π/n、Sin<S<Sout から
(1/2)sin(π/n)<(1/2)(π/n)<(1/2)tan(π/n)
2n倍して
nsin(π/n)<π<ntan(π/n)を導く*1
lim(n→∞)nsin(π/n)
x=(π/n)、n=(π/x)
lim((x=(π/n))→0)(π/x)sinx=π
lim(n→∞)ntan(π/n)
x=(π/n)、n=(π/x)
lim((x=(π/n))→0)(π/x)tanx=π
円の半径r
内接4角形の1辺の長さa=√2r(1-1-√2三角形より)、内接4角形の4辺の長さ4√2r
円の面積2πr
外接4角形1辺の長さb=円の直径2r、外接4角形4辺の長さ8r
4√2r<2πr<8r
2√2<π<4
したがって*1のn=4の時が上記の場合だから
4sin(π/4)<π<4tan(π/4)
2√2<π<4
終了
3.14<π<3.145を示せ
三角形の面積から求めると
Sin=(1/2)sinθ, S=(1/2)θ, Sout=(1/2)tanθ
となり、ここで θ=π/n, Sin<S<Sout から
(1/2)sin(π/n)<(1/2)(π/n)<(1/2)tan(π/n)
2n倍して
nsin(π/n)<π<ntan(π/n) ・・・*1
lim(n→∞)nsin(π/n)
x=(π/n)、n=(π/x)
lim((x=(π/n))→0)(π/x)sinx=π
lim(n→∞)ntan(π/n)
x=(π/n)、n=(π/x)
lim((x=(π/n))→0)(π/x)tanx=π
半角公式
sin^2(θ/2)=(1-cosθ)/2
cos^2(θ/2)=(1+cosθ)/2
tan^2(θ/2)=(1-cosθ)/(1+cosθ)
cos(π/8)=√((1+cos(π/4))/2)=√((1+√2/2)/2)=0.923879532511
cos(π/16)=√((1+cos(π/8))/2)=√((1+0.923879532511)/2)=0.9807852804
cos(π/32)=√((1+cos(π/16))/2)=√((1+0.9807852804)/2)=0.995184726672
sin(π/64)=√((1-cos(π/32))/2)=√((1-0.995184726672)/2)=0.049067674327418
64sin(π/64)=3.1403311569547529123171185243317
tan(π/64)=√((1-cos(π/32))/(1+cos(π/32)))=√((1-0.995184726672)/(1+0.995184726672))
=0.049126849769467
64tan(π/64)=3.144118385245904262741972561364
したがって*1のn=64の時
64sin(π/64)<π<64tan(π/64)
3.1403311569547529123171185243317<π<3.1441183852459042627419725613641
終了
2倍角
cos2α=2cos^2α-1
4倍角
cos4α=2cos^2 2α-1=2(2cos^2α-1)^2-1
以下同様
1/2倍角
cosα=√((cos2α+1)/2)
1/4倍角
cosα=√((√((cos4α+1)/2)+1)/2)
以下同様
pai.zip
paiサンプルソース
ここら辺の倍角だけでπを用いないcosテーブルを作った
なぜか、13倍角以上がエラーになる
リーマン予想
π
=lim(n→∞)nsin(π/n)
=lim(n→∞)Σ↑∞↓n=1 ((-1)^n/2n+1)
=lim(n→∞)√(6 Σ↑∞↓n=1 (1/n^2))
=lim(p→∞)√(6 Π↓p (1/(1-1/p^2)))
でようするに
π
=lim(n→∞)nsin(π/n)
なんだから
sinテーブル(波)を考えつつ
sin(π/n)×n=π
ってことは
何がいいたいかは分かるだろ
0<x<π/4に注目して
半角公式
sin(θ/2)=√((1-cosθ)/2)
cos(θ/2)=√((1+cosθ)/2)
にほかならない
だから、πを用いないでcosxテーブル書けたから
相対論に引き続きリーマン予想も俺が解いた
PrimeNumber.zip
カンニング素数判定サンプルソース
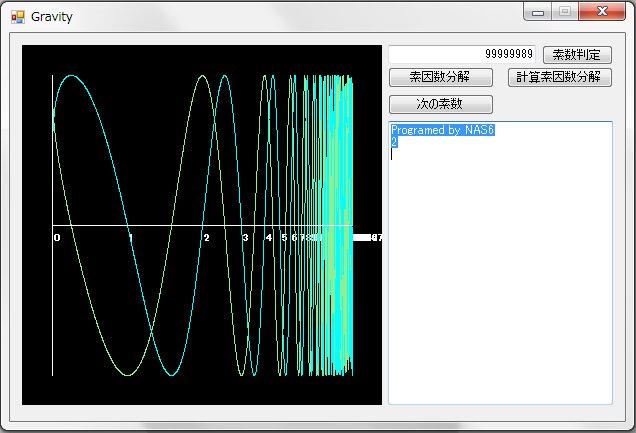
cosπx,sinπxの横軸対数グラフ
無限大の有限化
範囲は
0<a<MAX_N
0<x<∞
0<Θ<2πの範囲のsinカーブがあって
x=log↓2 Θの軸で0<x<∞の実数界が出来て・・・
結局sin波の重ね合わせでしょ
Π↓p→x,x→1,2,3,・・・,∞ sin πx/p ≠ 0 = π(p+1)
π(13)=sin πx/2 * sin πx/3 * sin πx/5 * sin πx/7 * sin πx/11 ≠ 0
sin πx/2 = 0 (2,4,6,8,10・・・)
sin πx/3 = 0 (3,6,9,12・・・)
以下同様
ようするにエラトステネスのふるい
これは、実数界であったり、素数であったり、πであったり、波動関数であったりします
これが、再帰的に入っているだけです
再帰的に入れるにあたって、半角公式で再帰しています
1/2倍角
cosα=√((cos2α+1)/2)
1/4倍角
cosα=√((√((cos4α+1)/2)+1)/2)
以下同様
半角再帰だから、対数グラフになっています
無限の有限証明
lim↓x→∞ x
MAX_N=任意
n=MAX_N
c=MAX_N/x
lim↓x→∞ c=0
c=無限のとき
a=0.0
それ以外
a = MAX_N * Math.Pow(1.0 / n, c)
lim↓c→0 a=MAX_N
d = x = MAX_N / (Math.Log(a / MAX_N) / Math.Log(1.0 / n))
b = Math.Cos((Math.PI * d) * (2.0 / MAX_N))
0<x<∞
0<a<MAX_N
無限を有限で表現できた
証明終了
ゼノンのパラドックスの完全解答
詰みきった
cosπx,sinπxの横軸対数グラフは、0が一番目盛幅が大きく、数が大きくなるにしたがって目盛幅が小さくなる
見た目でも、1mずつ印をつけた地面の0mから先を見ると同様になっている
要するに縮退していく宇宙と見える
で、素数ってエラストテネスの篩とか考えると
2×3=6でふるって
7以上の素数って6で割った余りは1、5が素数の必要条件で
2×3×5=30でふるって
31以上の素数って30で割った余りは1、7、11、13、17、19、23、29が素数の必要条件
6の場合、はじけないのは2/6、30の場合、はじけないのは8/30、210の場合、はじけないのは43/210
になるから、その素数単純判定法がめちゃくちゃ計算量が少ないんじゃないかなぁ・・・
同様に2×3×5×7=210でも2×3×5×7×11=2310でも
素数列を順番に掛け合わせれば出来るけど、コーディングのデータ入力が面倒くさいです
その場合は素数データファイルを作ってそれでやらせて、1以外の掛け合わした素数以外の素数がその必要条件
掛け合わす素数が大きくなるほど、よくはじきます
はじけない確率P、ガウスの素数確率G
G=1/ln6=0.55811
P=2/6=0.3333333
G=1/ln30=0.2940141
P=8/30=0.266666667
G=1/ln210=0.187017
P=43/210=0.2047619
テスト中
ああ、6、30、はよくて、210はうまくいかないで、2310はいい感じかも
どんな数でふるうかの法則がまだよく分からないな
6、30、しかだめかも・・・
P=8/30=0.266666667
x log(x) P=1/log(x)
10 2.303 0.4342
100 4.605 0.2172
1000 6.908 0.1447
10000 9.210 0.1086
100000 11.513 0.0869
ま、十分か
戻る



