衛星軌道計算フォーム(誤差がかなりあります) SatelliteOrbitCalcForm
惑星シミュレータ、自分で自由に設定した惑星/衛星の軌道が計算できます
惑星を選んで、上から順に計算して、値を適用していってください
入力(速度計算:単位、AU、年)(デフォルト値:水星) input(CalcVelocity:unit:AU,year)(default:Mercury)
衛星離心率 e = eccentricity e
衛星近日点距離 RA1(AU) = perihelion RA1(AU)
衛星遠日点距離 RA2(AU) = aphelion RA2(AU)
衛星軌道1 R1(AU)(計算基準) = orbit1 R1(AU)(calcBase)
衛星軌道2 R2(AU) = orbit2 R2(AU)
衛星質量 M2(kg) = satellite mass M2(kg)
公転周期 P(年) = orbital period P(year)
重力源質量 M1(kg) = attractor mass M1(kg)
入力(速度計算:単位、m、s)(デフォルト値:水星) input(CalcVelocity:unit:m,s)(default:Mercury)
衛星離心率 e = eccentricity e
衛星近日点距離 RA1(m) = perihelion RA1(m)
衛星遠日点距離 RA2(m) = aphelion RA2(m)
衛星軌道1 R1(m)(計算基準) = orbit1 R1(m)(calcBase)
衛星軌道2 R2(m) = orbit2 R2(m)
衛星質量 M2(kg) = satellite mass M2(kg)
公転周期 P(s) = orbital period P(s)
重力源質量 M1(kg) = attractor mass M1(kg)
座標反転 reverse position
計算 Calc
天文単位 AU(m) = AU(m)
面速度/地球の面速度 Vst = face velocity rate
衛星近日点速度 VA1(m/s) = perihelion VA1(m/s)
衛星遠日点速度 VA2(m/s) = aphelion VA2(m/s)
衛星軌道1速度 V1(m/s) = orbit1 V1(m/s)
衛星軌道2速度 V2(m/s) = orbit2 V2(m/s)
入力(速度計算)(衛星軌道1)(デフォルト値:水星) Input(CalcVelocity)(orbit1)(default:Mercury)
重力源質量 M1(kg) = attractor mass M1(kg)
衛星質量 M2(kg) = satellite mass M2(kg)
衛星軌道2 R2(m) = orbit2 R2(m)
衛星軌道2速度 V2(m/s) = orbit2 velocity V2(m/s)
衛星軌道1 R1(m) = orbit1 R1(m)
計算 Calc
万有引力定数 G = gravitational constant
衛星軌道2力 F2(N) = orbit2 force F2(N)
衛星軌道2位置エネルギー U2(J) = orbit2 potential energy U2(J)
衛星軌道2エネルギー E2(J) = orbit2 energy E2(J)
衛星軌道1力 F1(N) = orbit1 force F1(N)
衛星軌道1位置エネルギー U1(J) = orbit1 potential energy U1(J)
衛星軌道1速度 V1(m/s) = orbit1 velocity V1(m/s)
入力(ケプラー方程式)(衛星軌道1)(デフォルト値:水星) Input(Kepler equation)(orbit1)(default:Mercury)
時間 t(s) = time t(s)
衛星離心率 e = eccentricity e
衛星軌道長半径 a(m) = semi-major axis a(m)
衛星公転周期 T(s) = orbital period T(s)
衛星元期 T*(s) = epoch T*(s)
衛星元期平均近点角 l(t*)(rad) = epoch mean anomaly l(t*)(rad)
微増時間 dt(s) = delta time dt(s)
計算 Calc
衛星平均運動 n = mean motion n
衛星平均近点角 l(t)(rad) = mean anomaly l(t)(rad)
衛星離心近点角 u(t)(rad) = eccentric anomaly u(t)(rad)
衛星座標 X(m) = position X(m)
衛星座標 Y(m) = position Y(m)
衛星距離 R(m) = distance R(m)
衛星微増座標 dX(m) = delta position dX(m)
衛星微増座標 dY(m) = delta position dY(m)
衛星速度 V(m/s) = velocity V(m/s)
入力(相対論・オイラー法・ルンゲ・クッタ法)(衛星軌道1)(デフォルト値:水星) Input(Relative Euler RngKt)(orbit1)(default:Mercury)
微増時間デルタTが大きいと誤差が出ます
水星、連星パルサーの摂動確認はCalc5で行ってください
他の惑星の影響のない水星の摂動の理論値は5.023366e-7radです
dt=3600の場合、250Lapsくらいから、だんだん精度よく収束していきます
また、連星パルサーの摂動観測値は6.9927774e-5radです
衛星平均近点角 l(t)(rad) = 0 の時に
衛星離心率 e < 0.85 くらいまでならば、 MV ADJUST で軌道調整できます
重力源質量 M1(kg) = attractor mass M1(kg)
衛星質量 M2(kg) = satellite mass M2(kg)
衛星近日点距離 RA1(m) = perihelion RA1(m)
衛星遠日点距離 RA2(m) = aphelion RA2(m)
衛星軌道長半径 a(m) = semi-major axis a(m)
初速度倍率 mv0 = multiple velocity mv0
微増時間 dt(s) = delta time dt(s)
時間 t0(s) = time0 T0(s)
衛星座標 X(m) = position X(m)
衛星座標 Y(m) = position Y(m)
衛星速度 VX(m/s) = velocity VX(m/s)
衛星速度 VY(m/s) = velocity VY(m/s)
通知平均摂動下限 nth0(rad) = Notice Theta nth0(rad)
通知平均摂動上限 nth1(rad) = Notice Theta nth1(rad)
計算(オイラー法) Calc(Euler)
時間 t(s) = time T(s)
衛星座標 X2(m) = position X2(m)
衛星座標 Y2(m) = position Y2(m)
衛星速度 VX2(m/s) = velocity VX2(m/s)
衛星速度 VY2(m/s) = velocity VY2(m/s)
衛星速度 V2(m/s) = velocity V(m/s)
衛星周回数 Lap = Lap
衛星摂動 theta1(rad) = Theta1(rad)
衛星摂動 theta2(rad) = Theta2(rad)
衛星平均摂動 theta(rad) = Theta(rad)
計算(ルンゲ・クッタ法) Calc(RngKt)
時間 t(s) = time T(s)
衛星座標 X2(m) = position X2(m)
衛星座標 Y2(m) = position Y2(m)
衛星速度 VX2(m/s) = velocity VX2(m/s)
衛星速度 VY2(m/s) = velocity VY2(m/s)
衛星速度 V2(m/s) = velocity V(m/s)
衛星周回数 Lap = Lap
衛星摂動 theta1(rad) = Theta1(rad)
衛星摂動 theta2(rad) = Theta2(rad)
衛星平均摂動 theta(rad) = Theta(rad)
5-1:Schwarzschild,5-2:Kerr,5-3:LightDelay
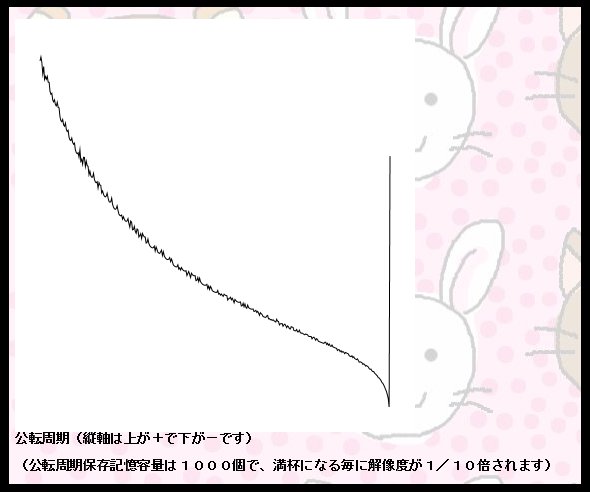
公転周期(縦軸は上が+で下が-です)
(公転周期保存記憶容量は1000個で、満杯になる毎に解像度が1/10倍されます)

水星摂動
dt=3600の時の例です
他の惑星の影響のない水星の摂動の理論値は5.023366e-7radです

連星パルサー PSR B1913+16摂動
dt=15の時の例です
連星パルサー PSR B1913+16の摂動の観測値はφ=4.22659°/年=0.07376791rad/年
公転周期P=0.0009473195年
P'=1/P=1055.6101周/年
φ/P'=6.9927774e-5radです
公転周期の縦軸は上が+で下が-ですので時間減衰しています
連星パルサー PSR B1913+16公転周期
dt=500の時の公転周期グラフです

連星パルサー PSR J0737-3039公転周期
dt=200の時の公転周期グラフです
私の方程式は、シュワルツシルト計量を用いているので、
これで分かる通り、離心率が大きいと誤差が出て、下に突のグラフになっています
正しくは上に突のグラフです
だから、円軌道のシュワルツシルト計量ではなく
楕円軌道の同様の計量を解けば完璧です
あー、カー解解くのか
んで、カー解はシュワルツシルト解の軌道を真円にすれば良いから
r半径,G万有引力定数,M質量1,m質量2,v軌道速度,c光速度,a軌道長半径
周期P=2.0*π*√(a^3/G(m+M))
軌道速度V=(a/P)*2.0*π/c
半径R=(m+M)*G/(V^2*c^2)=a
座標X=R
座標Y=0
座標法線nrmx=X/R
座標法線nrmy=Y/R
速度VX=V*nrmy
速度VY=V*nrmx
この条件でシュワルツシルト解を解けばいい
シュワルツシルト解Fshw=m(-GM/r^2)(1.0+3.0(v/c)^2)
そもそも、シュワルツシルト解から求めるカー解の導出法で座標変換をするので、こんな感じなのだろう
カー解導出シュワルツシルト解座標変換
t=t+2mlog|(r/2m)-1|、r=r、θ=θ、ψ=ψ
↓
t=t、r=a、θ=θ、ψ=ψ
半径r=軌道長半径a
だから
もちろん周期P=P
ゆえに運動量が変わらず正準変換を満たしてる

連星パルサー PSR B1913+16公転周期
5-2:カー解、dt=1500の時の公転周期グラフです
ええっ、座標変えたら意味ないじゃんと思う気もしますが
カー解を真面目にちゃんと解いてパラメータ処理してもカー解は真円運動に変換する式で
自分の式変形が不安だからシュワルツシルト解に戻しました
カー解の導出法で座標変換して真円運動にしていたんです
シュワルツシルト解
vポテンシャル、M質量、r距離、L角運動量
v^2(r)=(1-2M/r)(1+L^2/r^2)
u=1/r
u'^2=1-2Mu+u^2L^2-2ML^2u^3
u微分して
2u'u''=2Mu'-2u'uL^2+6ML^2u^2u'
u''+u=M-3ML^2u^2
カー解
vポテンシャル、M質量、r距離、L角運動量
V±(r)=((2Mra±r^2Δ^(1/2))/((r^2+a^2)^2-a^2Δ)))L
u=1/r,a=J/M,Δ=r^2-2Mr+a^2=1/u^2-2M/u+(J/M)^2
u'^2=((2J/u±(1/u^2)Δ^(1/2))/((1/u^2+(J/M)^2)^2-(J/M)^2Δ)L
=((2J/u±(1/u^2)Δ^(1/2))/(1/u^4+2(J/M)^2/u^2+(J/M)^4-(J/M)^2Δ)L
u微分して(Δ'=1/2u^3-2M/u^2)
2u''=((2J/u^2±(1/4u^3)Δ'^(-1/2))/(1/4u^5+(J/M)^2/u^3-(J/M)^2Δ')L
u''=((J/u^2±(1/8u^3)Δ'^(-1/2))/(1/4u^5+(J/M)^2/u^3-(J/M)^2Δ')L
=((J/u^2±(1/8u^3√(1/2u^3-2M/u^2))/(1/4u^5+(J/M)^2/u^3-(J/M)^2(1/2u^3-2M/u^2))L
=(M^2L/J)(1±(1/8Ju√(1/2u^3-2M/u^2))/(1/4u^3(J/M)^2+1/u-(1/2u)-2M))
F力=dv/dr
F±(r)=m(-GM/r^2) [(1±[r^2/8GM√(r^3(1/2)-2Mr^2)]) / ((r^3)/4(G/r)^2+r/2-2M)]
/ ((r^3)/4(G/r)^2+r/2-2M))の部分が真円運動に直している
ただ式変形に自信がないから使わないけど、多分どっか間違えてる
Δ'の微分係数とかかなり怪しい
どんな振る舞いするか見たくて、ざっと解いたら真円運動にしていた
注釈:uで微分:u=1/rと置いてあるからdu=-dr
光路差ガリレオ万有引力LightDelay(Calc5-3 RUN)
単純に距離/光速度=時差から
主星の座標を伴星の-速度×時差だけずらしてガリレオ万有引力で計算
(速度合成則は特殊相対論を用いた)
で、なんか、シュワルツシルト解と似たような振る舞いになった
戻る




