３Ｄプログラミング入門講座・その９：物理演算その１・電卓で相対性理論を解く方法



相対性理論的ニュートン力学
太陽系惑星軌道計算シミュレーターフォーム by javascript
相対性理論衛星軌道計算シミュレーターフォーム by javascript




電卓で相対性理論を解く方法


ｅ離心率Ｖ軌道速度Ｃ光速度として

特殊相対性理論補正項ＳＡは

ＳＡ＝(－０.５)(Ｖ／Ｃ)＾２

Ｆ＝－(ＧｍＭ／Ｒ＾２)(１＋ＳＡ)＝－(ＧｍＭ／Ｒ＾２)(１＋(－０.５)(Ｖ／Ｃ)＾２)


一般相対性理論補正項ＳＢは

ＳＢ＝(３.０)(Ｖ／Ｃ)＾２

Ｆ＝－(ＧｍＭ／Ｒ＾２)(１＋ＳＢ)＝－(ＧｍＭ／Ｒ＾２)(１＋(３.０)(Ｖ／Ｃ)＾２)


特殊と一般合わせた相対性理論補正項ＳＣ

ＳＣ＝(２.５)(Ｖ／Ｃ)＾２

Ｆ＝－(ＧｍＭ／Ｒ＾２)(１＋ＳＣ)＝－(ＧｍＭ／Ｒ＾２)(１＋(２.５)(Ｖ／Ｃ)＾２)


これを電卓でポチポチやれば解けます
しかし正しく単位合わせをごにょごにょする必要があります

楕円軌道の考察は後述


ｒｓ中心天体のシュバルツシルト半径ａ衛星の軌道長直径
また(Ｖ／Ｃ)＾２＝ｒｓ／ａの関係も成立します


一連の流れをまとめた証明はこちら


軌道束縛条件保存則

G万有引力定数M中心天体の質量c光速a軌道長半径e離心率V平均軌道速度dφ近日点移動
rs中心天体のシュワルツシルト半径(1/(1-e^2))真円軌道→楕円軌道変換

rsc^2=2GM=2aV^2=2a^3ω^2=ac^2(1-e^2)dφ/3π

自然なほかに外力が加わっていない万有引力運動であれば

この関係性が表れます

rsc^2=2GM
rsc^2=2aV^2
rsc^2=2a^3ω^2
rsc^2=ac^2(1-e^2)dφ/3π
これら右辺の計算は全てrsc^2の関係だったんです

但しdφの扱いには注意が必要でありrsを求めるには
1周の蓄積が必要であり2πをかける必要があるので
これに関してはこれが正解です
rsc^2=2ac^2(1-e^2)dφ/3
(1-e^2)の項は楕円軌道の一周の積分定数のようなものです

この関係性から代表的なものは
シュワルツシルト半径rs=2GM/c^2
軌道速度V=√(GM/a)=aω
ケプラー第3法則GM=a^3ω^2
近日点移動dφ=6πGM/ac^2(1-e^2)
などが求められます

また
rsc^2=2GM=2aV^2=2a^3ω^2=ac^2(1-e^2)dφ/3π
これらが各項に表れた等式
rsc^2,2GMなどを含む等式は
rsc^2,2GMなどについて解けばこの関係性に結び付けられます

例えば

1. 周期 T との関連
軌道長半径 a と、平均軌道速度 V または平均角速度 ω が含まれていますこれらの間には周期 T が関わってきます
ニュートン力学におけるケプラーの第3法則は通常以下の形で表されます
T^2=4π^2a^3/GM
この式をGMについて解くと
GM=4π^2a^3/T^2
rsc^2=2GMを使うと
rsc^2=2(4π^2a^3)/T^2
ここから得られる新しい等式
rsc^2=8π^2a^3/T^2
これは中心天体の重力特性rsc^2が軌道長半径aと周期Tという軌道の幾何学的な特徴と時間的な特徴だけで表現できることを示しています
古典的なケプラーの第3法則に相対論的な rsc^2 の概念を導入しているとも言えます

2. 近日点速度Vpと遠日点速度Vaとの関連
楕円軌道では近日点と遠日点で速度が異なりますこれらを式に組み込むことでより詳細な関係が見えてくるかも
エネルギー保存則（ニュートン力学）から近日点（rp = a(1-e)）と遠日点（ra = a(1+e)）での速度は以下のように表せます
Vp^2=(GM/a)((1+e)/(1-e))
Va^2=(GM/a)((1-e)/(1+e))
これらの式にGM=rsc^2/2を代入すると
Vp^2=(rsc^2/(2a))((1+e)/(1-e))
Va^2=(rsc^2/(2a))((1-e)/(1+e))
ここから得られる可能性のある等式
rsc^2=(2aVp^2(1-e))/(1+e)
rsc^2=(2aVa^2(1+e))/(1-e)
これらの式は近日点または遠日点における局所的な速度からrsc^2を求める方法を示唆しています
特に離心率eが大きい軌道でこれらの局所的な速度が相対論効果にどう影響するかを考える上で有用かも

3. 角運動量h(単位質量あたり)との関連
単位質量あたりの角運動量hも楕円軌道では保存される量です
h^2=GMa(1-e^2)
これを結びつけてみる
GM=rsc^2/2なので
h^2=(rsc^2/2)a(1-e^2)
ここから得られる新しい等式
rsc^2=(2h^2)/(a(1-e^2))
この等式は軌道の角運動量hと軌道長半径a離心率eからrsc^2を求める方法を示しています
角運動量という重要な保存量を通して重力場の特性rsc^2が表現できるのは非常に興味深い点です

4. エネルギーE(単位質量あたり)との関連
楕円軌道における単位質量あたりのエネルギーEも考えてみる
E=-GM/2a
これをGMについて解くと
GM=-2aE
rsc^2=2GMを使うと
rsc^2=2(-2aE)
ここから得られる新しい等式
rsc^2=-4aE
これは軌道長半径aと軌道のエネルギーEからrsc^2を求める方法を示しています
エネルギーという最も基本的な保存量を通して重力場の特性 rsc^2 が表現できるのは非常にエレガントです


つまりまとめて
G万有引力定数M中心天体の質量c光速a軌道長半径e離心率V平均軌道速度dφ近日点移動
rs中心天体のシュワルツシルト半径(1/(1-e^2))真円軌道→楕円軌道変換
T周期ω平均角速度Vp近日点速度Va遠日点速度
h角運動量(単位質量あたり)Eエネルギー(単位質量あたり)

rsc^2=2GM=2aV^2=2a^3ω^2=ac^2(1-e^2)dφ/3π=8π^2a^3/T^2

=(2aVp^2(1-e))/(1+e)=(2aVa^2(1+e))/(1-e)=(2h^2)/(a(1-e^2))=-4aE

のように様々な関係性が導かれます
念のため単位を確かめてみる[m^3s^-2]であればたぶん成立するので
8π^2a^3/T^2=[m^3s^-2]
(2aVp^2(1-e))/(1+e)=(2aVa^2(1+e))/(1-e)=[m^3s^-2]
(2h^2)/(a(1-e^2))=[m^3s^-2]
-4aE=[m^3s^-2]

つまり中心天体の質量による軌道と形状のエネルギー保存則は
シンプルに運動エネルギー
E=-(rs/4a)c^2=-GM/2a
であるということです

そりゃあエネルギー保存則は
運動エネルギー＋位置エネルギーなのだから
位置エネルギーを解放したら運動エネルギーだよな

∫[dE/da]dm=-GMm/a^2=F
でふりだしに戻って相対性理論は古典力学に統合されました
dφ=(3/(1-e^2))(v/c)^2として
F=(-GMm/a^2)(1+(3/(1-e^2))(v/c)^2)=(-GMm/a^2)(1+dφ)
を思い出すとF=∫[dE/da]dmは
F=(∫[dE/da]dm)(1+(3/(1-e^2))(v/c)^2)=(-GMm/a^2)(1+(3/(1-e^2))(v/c)^2)=(-GMm/a^2)(1+dφ)
なのだからつまり正確に記述すると
E=(-GM/2a)(1+(3/(1-e^2))(v/c)^2)=(-GM/2a)(1+dφ)
rsc^2=-4aEに代入して
rsc^2=2GM(1+(3/(1-e^2))(v/c)^2)=2GM(1+dφ)つまり
G万有引力定数M中心天体の質量c光速a軌道長半径e離心率V平均軌道速度dφ近日点移動
rs中心天体のシュワルツシルト半径(1/(1-e^2))真円軌道→楕円軌道変換
T周期ω平均角速度Vp近日点速度Va遠日点速度
h角運動量(単位質量あたり)Eエネルギー(単位質量あたり)

dφ=(3/(1-e^2))(v/c)^2として

rsc^2=2GM=2aV^2(1+dφ)=2a^3ω^2(1+dφ)

=ac^2(1-e^2)dφ(2/3)=(8π^2a^3/T^2)(1+dφ)

=(2aVp^2(1-e))(1+dφ)/(1+e)=(2aVa^2(1+e))(1+dφ)/(1-e)

=(2h^2)(1+dφ)/(a(1-e^2))=-4aE(1+dφ)=[m^3s^-2]

とこれが正確な記述であるとしてdφ=(3/(1-e^2))(v/c)^2は
(惑星名, 軌道長半径a[m], 平均軌道速度V[m/s], 離心率e, (1-e^2), 3.0/(1-e^2), (v/c)^2, dφ, 2πdφ, rs=a(1-e^2)2πdφ/3, rs=(a(1-e^2)2πdφ/3π)(1+dφ))
(水星, 57909656770, 47872.5, 0.2056, 0.95772864, 3.1324112851, 2.5499449799789e-8, 7.98747643167e-8, 5.018679455692e-7, 2953.328771, 2953.329)
水星の場合はdφ=7.98747643167e-8なので1+dφは上位から8桁目に寄与する微小な補正項である

dφ=(3/(1-e^2))(v/c)^2として
rsc^2=2GM=2aV^2(1+dφ)=2a^3ω^2(1+dφ)
=ac^2(1-e^2)dφ(2/3)=(8π^2a^3/T^2)(1+dφ)
=(2aVp^2(1-e))(1+dφ)/(1+e)=(2aVa^2(1+e))(1+dφ)/(1-e)
=(2h^2)(1+dφ)/(a(1-e^2))=-4aE(1+dφ)=[m^3s^-2]
ここから導出される
rs=2GM/c^2
V=√(GM/a(1+dφ))=aω/√(1+dφ)
GM=a^3ω^2(1+dφ)
T=√((4π^2a^3/GM)(1+dφ))
h=√(GMa(1-e^2)/(1+dφ))
E=-GM/4a(1+dφ)
は問題ありませんが
dφ=3GM/ac^2(1-e^2)
は2πが消えて1ラジアンあたりになっています


特殊の証明＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃

ローレンツ収縮
a=√(1-(v/c)^2)
の近似は
a=1-0.5(v/c)^2
です

FA(v)=√(1-(v/c)^2)
FB(v)=1-0.5(v/c)^2

FA(1.0c)=0
FB(1.0c)=0.5

FA(0.99c)=0.14
FB(0.99c)=0.49

FA(0.8c)=0.6
FB(0.8c)=0.68

FA(0.5c)=0.866
FB(0.5c)=0.875

FA(0.2c)=0.979
FB(0.2c)=0.98

FA(0.1c)=0.994
FB(0.1c)=0.995


一般の証明＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃

計量(ci,1,1,1)のシュワルツシルト(球対称性を持つアインシュタイン方程式の真空解)の線素は
ｃ光速度ｔ座標時ｒ動径座標θ余緯度座標φ経度座標2m=ｒｓシュワルツシルト半径＝２ＧＭ／ｃ＾２M質量
ds^2=(1-rs/r)c^2dt^2-dr^2/(1-rs/r)-r^2dθ^2-r^2sin^2θdψ^2
ds^2=(1-2m/r)c^2dt^2-dr^2/(1-2m/r)-r^2dθ^2-r^2sin^2θdψ^2･･･(*1)
その変分問題
δ∫((1-2m/r)c^2(dt/ds)^2-(dr/ds)^2/(1-2m/r)-r^2(dθ/ds)^2-r^2sin^2θ(dψ/ds)^2)ds=0･･･(*2)
各成分に対する方程式を導出すると
i=1,r,(*1)/ds^2
1=(1-2m/r)c^2(dt/ds)^2-(dr/ds)^2/(1-2m/r)-r^2(dθ/ds)^2-r^2sin^2θ(dψ/ds)^2･･･(*1A)
i=2,θ,
(d/ds)(r^2(dθ/ds))=r^2sinθcosθ(dψ/ds)^2･･･(*1B)
i=3,ψ,
(d/ds)(r^2sin^2θ(dψ/ds))=0･･･(*1C)
i=0,ct
(d/ds)((1-2m/r)(dt/ds))=0･･･(*1D)
成分を選んで
θはπ/2、dθ/ds=0、の赤道面上での話とし、θは定数なので(*1B)は無視する
ψは(*1C)よりr^2(dψ/ds)=h(定数)角運動量保存･･･(*3)
tは(*1D)より(1-2m/r)(dt/ds)=l(定数)エネルギー量保存･･･(*4)
(*1A)より
(1-2m/r)=(cl)^2-(dr/ds)^2-(h/r)^2(1-2m/r)･･･(*5)
rをψの関数として微分したものは
(d/dψ)(r(ψ))=r'=(dr/ds)(ds/dψ),(*3)より
(dr/ds)=r'(dψ/ds)=hr'/r^2,r=1/u,r'=-u'/u^2,(*5)より
(1-2mu)=(cl)^2-(hu')^2-(hu)^2(1-2mu)
u'^2=((cl)^2-1)/h^2+2mu/h^2-u^2+2mu^3･･･(*6)
ψで微分して
2u'u''=2mu'/h^2-2uu'+6mu^2u'･･･(*7)
u'=0,u=1/r(定数)という解は円軌道
u''+u=m/h^2+3mu^2･･･(*8)
この式はu''+u=m/h^2が万有引力の式に対応しイメージしてみると
シュワルツシルト時空の重力による加速度RelativeGravityの式は
r半径,G万有引力定数,M質量,V軌道速度,c光速度,S相対論補正項
Rg=-(GM/r^2)(1+S)
の形であるから、ここでh=r^2dψ/ds,m=kM/c^2,u=1/r,であって
相対論補正項3mu^2を検証すると、m/h^2でくくり
u''+u=(m/h^2)(1+3mu^2/(m/h^2)=(m/h^2)(1+S)の形にして、Sを調べます
3mu^2/(m/h^2)=3u^2h^2=3(1/r^2)(r^2dψ/ds)^2=3r^2((dt/ds)(dψ/dt))^2=3r^2(dψ/dt)^2(1/c^2)
=3(rdψ/dt)^2(1/c^2)
(rdψ/dt)は円の接線方向の速度だからそれを軌道速度Vとみれば3(V/c)^2と解けて
相対論補正項S=3(V/c)^2だから
ユークリッド幾何で
シュワルツシルト時空の重力による加速度RelativeGravityの式は
r半径,G万有引力定数,M質量,V軌道速度,c光速度,S相対論補正項
Rg=-(GM/r^2)(1+S)=-(GM/r^2)(1+3(V/c)^2)
と解ける

＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃

ここから楕円軌道の補正(1-e^2)など一周の積分定数を考える必要がある場合もある

楕円軌道の場合は
特殊相対性理論ＳＡ
Ｆ＝－(ＧｍＭ／Ｒ＾２)(１＋(‐０.５)(Ｖ／Ｃ)＾２)
＝－(ＧｍＭ／Ｒ＾２)(１＋ＳＡ)
ＳＡ＝(－０.５)(Ｖ／Ｃ)＾２
一般相対性理論ＳＢ
Ｆ＝－(ＧｍＭ／Ｒ＾２)(１＋(３.０)(Ｖ／Ｃ)＾２)
＝－(ＧｍＭ／Ｒ＾２)(１＋ＳＢ)
ＳＢ＝(３.０)(Ｖ／Ｃ)＾２
特殊と一般合わせてＳＣ
Ｆ＝－(ＧｍＭ／Ｒ＾２)(１＋(２.５)(Ｖ／Ｃ)＾２)
＝－(ＧｍＭ／Ｒ＾２)(１＋ＳＣ)
ＳＣ＝(２.５)(Ｖ／Ｃ)＾２

であって係数は本質ではないと考えると
相対性理論補正項Ｓは
Ｓ＝(Ｖ／Ｃ)＾２
であってこの意味するところは相対性理論は
速度による空間の慣性抵抗であると考えられる

計算例

地球質量5.972e+24kg
地球半径6.371e+6[m]
光速度299792458[m/s]
一日86400[s]

GPS衛星
速度4000[m/s]
高度26556752[m]

特殊相対論効果-7.2e-6[s/day]
一般相対論効果45.6e-6[s/day]
足して38.4e-6[s/day]


相対論補正項は

特殊
－０.５（Ｖ／Ｃ）＾２＝-8.9e-11
一日当たり
-8.9e-11*86400=-7.69e-6

一般
３.０（Ｖ／Ｃ）＾２＝5.34e-10
一日当たり
5.34e-10*86400=4.61e-5

特殊＋一般
２.５（Ｖ／Ｃ）＾２＝4.45e-10
一日当たり
4.45e-10*86400=3.85e-5

と微分方程式を解かずとも
電卓を何回か弾くだけで簡単に解けます

検証
F=-(GmM/r^2)(1+αV)の形に
なっているので
相対性理論補正とは
いわゆる慣性抵抗となっていて
通常の相対性理論では
同時の相対性(物体毎に時間軸がある)により
時刻合わせが大変で
世界を一つの画面で
表現する事は難しいのですが
これはユークリッド幾何と
なっているため
絶対時間の表現なので
世界を一つの画面で
表現出来ます

注釈：
上の計算では
時空の3+1分解というかもっと簡単に
極座標のr=√(x^2+y^2+z^2)
についての一日当たりの円周上の相対論補正項
を求めています



F=-(GmM/r^2)(1+S)のグラフ概要

赤色と水色の合成みたいな軌跡です

F=-(GmM/r^2)(1+S)が一般相対論の要請通りに
花びら落下の軌跡を描くことの図解


一般相対性理論の要請通りに重力波を放出して最終的には落下するという軌跡を描きます
ただし落下するには天文学的な周回が必要です
一般相対論の軌道の要請は
・花びら落下軌道
つまり
楕円軌道が進行方向に歪み徐々に高度を落としていく
というものです
相対論補正項をめちゃくちゃに大げさにした↓のシミュレートで
その要請を満たすことが確認できます



F=-(GmM/r^2)(1+S)の重力波を放出して軌道が不安定になるシミュレート
G=6.67e-11,m=1,M=100,r=1[AU]
ルンゲクッタ法で計算しているので不安定になるのは多分丸め誤差のせいじゃないです
相対論効果と多体問題による摂動です

S = × (v/c)^2
SA = -0.5 × (v/c)^2：特殊相対性理論
SB = 3.0 × (v/c)^2：一般相対性理論
SC = 2.5 × (v/c)^2：一般相対性理論＋特殊相対性理論
S0 = 0.0 × (v/c)^2：古典万有引力
つまり
SB = -6SA
SC = -5SA



F=-(GmM/r^2)(1+S)
S=(3.0)(v/c)^2これを
S=(2.5e6)(v/c)^2として
大げさに相対論補正項を設定して
その振る舞いを見る

ちゃんとこういう軌道になっています


＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃
(＊Ａ)の考察

近日点移動理論値
dφ=2π(3/2)(a/l)=2π(3/2)(a/((L/2)(1-e^2)))[rad/周]
dφ=360*3600(3/2)(a/((L/2)(1-e^2)))[秒/周]*[周/年]*[年]

1[AU]=149598700000[m]
太陽のシュバルツシルト半径a=2953[m]

水星軌道速度47872.5[m/s]
水星の離心率e=0.20563
水星の軌道長半径L/2=0.3871[AU]
水星4.15[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒/100年]
dφ'=360*3600*3*(v/c)^2*4.15*100=360*3600*3*(47872.5/299792458)^2*4.15*100=41.14[秒/100年]

ここで
41.14/42.9=0.959
1-e^2=0.958
だから
(3/(1-e^2))*(v/c)^2
だとすると
dφ'=42.9
になるから相対論補正項は
(3/(1-e^2))*(v/c)^2？？？
この(1-e^2)の項は楕円軌道の一周の積分定数の項でした

なぜならば一般の証明から

Sを調べます
3mu^2/(m/h^2)=3u^2h^2=3(1/r^2)(r^2dψ/ds)^2=3r^2((dt/ds)(dψ/dt))^2=3r^2(dψ/dt)^2(1/c^2)
=3(rdψ/dt)^2(1/c^2)=3(v/c)^2
と
ψは(*1C)よりr^2(dψ/ds)=h(定数)角運動量保存･･･(*3)
より離心率ｅがあるとき
(dψ/ds)^2=(h/r^2)^2=1/(1-e^2)
となる

注
楕円面積S=πa^2√(1-e^2)
dS/dt=h一定=S/T=πa^2√(1-e^2)/T
だから
(dψ/ds)^2=X/(1-e^2)


上へ戻る


確かめ算

近日点移動理論値
dφ=2π(3/2)(a/l)=2π(3/2)(a/((L/2)(1-e^2)))[rad/周]
dφ=360*3600(3/2)(a/((L/2)(1-e^2)))[秒/周]*[周/年]*[年]
dφ'=360*3600*(3.0/(1-e^2))(v/c)^2[秒/周]*[周/年]*[年]

1[AU]=149598700000[m]
太陽のシュバルツシルト半径a=2953[m]

水星軌道速度47872.5[m/s]
水星の離心率e=0.20563
水星の軌道長半径L/2=0.3871[AU]
水星4.15[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒/100年]
dφ'=360*3600*3*(v/c)^2*4.15*100=360*3600*3*(47872.5/299792458)^2*4.15*100=41.14[秒/100年]
1-e^2=0.958
41.14/0.958=42.9

金星軌道速度35020[m/s]
金星の離心率e=0.0068
金星の軌道長半径L/2=0.7233[AU]
金星1.633[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.7233)/(1-0.0068^2)*1.633*100=8.6[秒/100年]
dφ'=360*3600*3*(v/c)^2*1.66*100=360*3600*3*(35020/299792458)^2*1.66*100=8.6[秒/100年]
1-e^2=0.99995
8.6/0.99995=8.6

地球軌道速度297800[m/s]
地球の離心率e=0.0167
地球の軌道長半径L/2=1.0[AU]
地球1.0[周/年]
dφ=360*3600*3/2*2953/(149598700000*1.0)/(1-0.0167^2)*1.0*100=3.83[秒/100年]
dφ'=360*3600*3*(v/c)^2*1.0*100=360*3600*3*(297800/299792458)^2*1.0*100=3.83[秒/100年]
1-e^2=0.9997
3.83/0.9997=3.83

火星軌道速度24130[m/s]
火星の離心率e=0.0934
火星の軌道長半径L/2=1.5237[AU]
火星0.53[周/年]
dφ=360*3600*3/2*2953/(149598700000*1.5237)/(1-0.0934^2)*0.53*100=1.34[秒/100年]
dφ'=360*3600*3*(v/c)^2*0.53*100=360*3600*3*(24130/299792458)^2*0.53*100=1.33[秒/100年]
1-e^2=0.991
1.33/0.991=1.34


だからまとめて整理すると



一般の証明＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃

計量(c,i,j,k)のシュワルツシルト(球対称性を持つアインシュタイン方程式の真空解)の線素は
ｃ光速度ｔ座標時ｒ動径座標θ余緯度座標φ経度座標2m=ｒｓシュワルツシルト半径＝２ＧＭ／ｃ＾２M質量
ds^2=(1-rs/r)c^2dt^2-dr^2/(1-rs/r)-r^2dθ^2-r^2sin^2θdψ^2
ds^2=(1-2m/r)c^2dt^2-dr^2/(1-2m/r)-r^2dθ^2-r^2sin^2θdψ^2･･･(*1)
その変分問題
δ∫((1-2m/r)c^2(dt/ds)^2-(dr/ds)^2/(1-2m/r)-r^2(dθ/ds)^2-r^2sin^2θ(dψ/ds)^2)ds=0･･･(*2)
各成分に対する方程式を導出すると
i=1,r,(*1)/ds^2
1=(1-2m/r)c^2(dt/ds)^2-(dr/ds)^2/(1-2m/r)-r^2(dθ/ds)^2-r^2sin^2θ(dψ/ds)^2･･･(*1A)
i=2,θ,
(d/ds)(r^2(dθ/ds))=r^2sinθcosθ(dψ/ds)^2･･･(*1B)
i=3,ψ,
(d/ds)(r^2sin^2θ(dψ/ds))=0･･･(*1C)
i=0,ct
(d/ds)((1-2m/r)(dt/ds))=0･･･(*1D)
成分を選んで
θはπ/2、dθ/ds=0、の赤道面上での話とし、θは定数なので(*1B)は無視する
ψは(*1C)よりr^2(dψ/ds)=h(定数)角運動量保存･･･(*3)
tは(*1D)より(1-2m/r)(dt/ds)=l(定数)エネルギー量保存･･･(*4)
(*1A)より
(1-2m/r)=(cl)^2-(dr/ds)^2-(h/r)^2(1-2m/r)･･･(*5)
rをψの関数として微分したものは
(d/dψ)(r(ψ))=r'=(dr/ds)(ds/dψ),(*3)より
(dr/ds)=r'(dψ/ds)=hr'/r^2,r=1/u,r'=-u'/u^2,(*5)より
(1-2mu)=(cl)^2-(hu')^2-(hu)^2(1-2mu)
u'^2=((cl)^2-1)/h^2+2mu/h^2-u^2+2mu^3･･･(*6)
ψで微分して
2u'u''=2mu'/h^2-2uu'+6mu^2u'･･･(*7)
u'=0,u=1/r(定数)という解は円軌道
u''+u=m/h^2+3mu^2･･･(*8)
この式はu''+u=m/h^2が万有引力の式に対応しイメージしてみると
シュワルツシルト時空の重力による加速度RelativeGravityの式は
r半径,G万有引力定数,M質量,V軌道速度,c光速度,S相対論補正項
Rg=-(GM/r^2)(1+S)
の形であるから、ここでh=r^2dψ/ds,m=kM/c^2,u=1/r,であって
相対論補正項3mu^2を検証すると、m/h^2でくくり
u''+u=(m/h^2)(1+3mu^2/(m/h^2)=(m/h^2)(1+S)の形にして、Sを調べます
3mu^2/(m/h^2)=3u^2h^2=3(1/r^2)(r^2dψ/ds)^2=3r^2((dt/ds)(dψ/dt))^2=3r^2(dψ/dt)^2(1/c^2)
=3(rdψ/dt)^2(1/c^2)
(rdψ/dt)は円の接線方向の速度だからそれを軌道速度Vとみれば3(V/c)^2と解けて
相対論補正項S=3(V/c)^2だから
ユークリッド幾何で
シュワルツシルト時空の重力による加速度RelativeGravityの式は
r半径,G万有引力定数,M質量,V軌道速度,c光速度,S相対論補正項
Rg=-(GM/r^2)(1+S)=-(GM/r^2)(1+3(V/c)^2)
と解ける

ただしこの説明は真円軌道の時

＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃
楕円軌道の証明

近日点移動理論値
dφ=2π(3/2)(a/l)=2π(3/2)(a/((L/2)(1-e^2)))[rad/周]
dφ=360*3600(3/2)(a/((L/2)(1-e^2)))[秒/周]*[周/年]*[年]

1[AU]=149598700000[m]
太陽のシュバルツシルト半径a=2953[m]

水星軌道速度47872.5[m/s]
水星の離心率e=0.20563
水星の軌道長半径L/2=0.3871[AU]
水星4.15[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒/100年]
dφ'=360*3600*3*(v/c)^2*4.15*100=360*3600*3*(47872.5/299792458)^2*4.15*100=41.14[秒/100年]

ここで
41.14/42.9=0.959
1-e^2=0.958
だから
(3/(1-e^2))*(v/c)^2
だとすると
dφ'=42.9
になるから相対論補正項は
(3/(1-e^2))(v/c)^2となるか？
この(1-e^2)の項は楕円軌道の一周の積分定数がこう出るのでした

なぜならば一般の証明から

Sを調べます
3mu^2/(m/h^2)=3u^2h^2=3(1/r^2)(r^2dψ/ds)^2=3r^2((dt/ds)(dψ/dt))^2=3r^2(dψ/dt)^2(1/c^2)
=3(rdψ/dt)^2(1/c^2)=3(v/c)^2
と


メモ：軌道速度、真円、楕円

真円の扇の面積Aはr,θ,軌道速度vで
A=(1/2)r^2θ=(1/2)rv
v=2A/r
v^2=4A^2/r^2
また質量M万有引力定数Gで
v=√(GM/r)
v^2=GM/r

楕円の扇の面積Bはq,ψ,軌道速度wで
B=(1/2)q^2ψ√(1-e^2)=(1/2)qw√(1-e^2)
w=2B/q√(1-e^2)
w^2=4B^2/q^2(1-e^2)
また質量N万有引力定数Gで
w=√(GN(1+e^2+2ecosψ)/q(1-e^2))
w^2=GN(1+e^2+2ecosψ)/q(1-e^2)

3(v/c)^2のvを楕円軌道速度で適用しようとすると
(1+e^2+2ecosψ)が加味されているので
楕円軌道速度と真円軌道速度と
真円軌道で求めた3(v/c)^2で
あと足りない部分を補完して
(3/(1-e^2))(v/c)^2となる


これが一般相対性理論の楕円軌道の相対論補正項つまりカー解の答えとなる


したがって

楕円軌道(離心率e)の一般相対性理論を考慮した万有引力運動方程式は
Ｆ＝－(ＧｍＭ／Ｒ＾２)(１＋(３.０)(Ｖ／Ｃ)＾２)
と解けました
Ｆ力Ｇ万有引力定数ｍＭ質点質量Ｒ質点間距離ｅ離心率Ｖ軌道速度Ｃ光速度

この一周の積分は(1-e^2)の積分定数の補正が必要な場合もある

証明終了
＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃


古い説明
ψは(*1C)よりr^2(dψ/ds)=h(定数)角運動量保存･･･(*3)
より離心率ｅがあるとき
(dψ/ds)^2=(h/r^2)^2=1/(1-e^2)
となる

注
楕円面積S'=πa^2√(1-e^2)
dS'/dt=h一定=S'/T=πa^2√(1-e^2)/T
だから
(dψ/ds')^2=X一定/(1-e^2)
ここで
h=r^2dψ/ds'
だから
h^2=r^4(dψ/ds')^2
(dψ/ds')^2=h^2/r^4
これは
dS'/dt=h一定=S/T=πa^2√(1-e^2)/T
(ds'/dψ)^2^2=h^2/r^4(1-e^2)
=T^2/π^2a^4(1-e^2)
=(T^2/S'^2)
T/S'=1/h一定
S'=πr^2が真円なので
楕円成分は(1-e^2)にかかっているので結局
相対論補正項S=3mu^2/(m/h^2)=3(rdψ/dt)^2(1/c^2)=(3/(1-e^2))(v/c)^2
となりました
つまりやっぱり楕円面積S'=πr^2√(1-e^2)ってこと


だから注のまとめは
楕円面積S'=πa^2√(1-e^2)であり
相対論補正項S=3mu^2/(m/h^2)=3(rdψ/dt)^2(1/c^2)=3(v/c)^2
だと真円面積S'^2だから(1-e^2)で割った
相対論補正項S=3mu^2/(m/h^2)=3(rdψ/dt)^2(1/c^2)=(3/(1-e^2))(v/c)^2
が正しい楕円軌道の相対論補正項となる


したがって

楕円軌道(離心率e)の一般相対性理論を考慮した万有引力運動方程式は
Ｆ＝－(ＧｍＭ／Ｒ＾２)(１＋(３.０)(Ｖ／Ｃ)＾２)
と解けました
Ｆ力Ｇ万有引力定数ｍＭ質点質量Ｒ質点間距離ｅ離心率Ｖ軌道速度Ｃ光速度

この一周の積分は(1-e^2)の積分定数の補正が必要な場合もある

証明終了
＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃＃


このように
リーマン幾何の一般相対論を
ユークリッド幾何でおらは解いたのだが
アインシュタイン以来百年間誰も解けなかったことを
せっかく解いたのに
これでなんで
おらはノーベル物理学賞を貰えていないのだろう？
幻覚もまあ見るけれど数学はちゃんと出来るのに
なんでただの基地外扱いされんの？
あと社会の法律なんかよりも
万有引力の法則は強制力が全然強いはずですよん
反権力で反戦平和と愛を歌う
転がる石ころロックだぜい
万有引力は究極の不自由(仕事)の中の究極の自由(遊び)だ
この証明のようにおらには絶大な自信がたっぷりある
別にただ単に地球の
相対論的な万有引力の
運動の式ってだけ
もしも万有引力に逆らいたかったら
危ないから紐付けてバンジージャンプでもしてみてね


相対性理論的ケプラー方程式も解けるかもな
kepler=u+duでduの誤差をなくしていくんだけど
普通のケプラー方程式に
relkepler=u+du+ds^2=u+du+(3/(1-e^2)(v/c)^2)
これで良いのではないかな？

面積速度一定ってつまり
向心力(重力引力)一定と同じだし
面積差分の二乗つまり
U=ma^2ってことだ

ちょっと違うな
U=(1/2)mv^2+mgh
ポテンシャルエネルギー一定やろ

それで結局E=mc^2になるな

つまりここだ
i=0,ct
(d/ds)((1-2m/r)(dt/ds))=0･･･(*1D)
tは(*1D)より(1-2m/r)(dt/ds)=l(定数)エネルギー量保存･･･(*4)


ちょっと思いつき
dφ=360*3600(3/2)(a/((L/2)(1-e^2)))*4.15*100=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒/100年]
dφ'=360*3600*(3/(1-e^2))*(v/c)^2*4.15*100=360*3600*(3/0.958)*(47872.5/299792458)^2*4.15*100=42.9[秒/100年]
だから
(3/2)(a/((L/2)(1-e^2)))=(3/(1-e^2))*(v/c)^2
(a/L)=(v/c)^2
実際に値を入れてみると
1[AU]=149598700000[m]
太陽のシュバルツシルト半径a=2953[m]

水星軌道速度47872.5[m/s]
水星の離心率e=0.20563
水星の軌道長半径L/2=0.3871[AU]
水星4.15[周/年]

(a/L)=(v/c)^2
(a/L)=2953/(0.3871*149598700000*2)=2.55e-8
(v/c)^2=(47872.5/299792458)^2=2.55e-8

ちゃんと出ました

この公式から色んなのが出来そう
だから例えば
楕円軌道(離心率e)の一般相対性理論を考慮した万有引力運動方程式は
Ｆ＝－(ＧｍＭ／Ｒ＾２)(１＋(３.０)(Ｖ／Ｃ)＾２)
と解けました
Ｆ力Ｇ万有引力定数ｍＭ質点質量Ｒ質点間距離ｅ離心率Ｖ軌道速度Ｃ光速度
は
楕円軌道(離心率e)の一般相対性理論を考慮した万有引力運動方程式は
Ｆ＝－(ＧｍＭ／Ｒ＾２)(１＋(３.０)(ａ／Ｌ))
と解けました
Ｆ力Ｇ万有引力定数ｍＭ質点質量Ｒ質点間距離ｅ離心率ａ太陽のシュバルツシルト半径Ｌ衛星の軌道長直径
と等価です


上へ戻る


メモ：相対論的速度合成則

・xブーストの相対論的速度合成則
任意の方向にするには
まずx軸へ速度ベクトルを回転させ
xブーストし元に戻せばいい

Vx'=(Vx-V)/(1-(VxV/c^2))
Vy'=(Vy)/γ(1-(VxV/c^2))
Vz'=(Vz)/γ(1-(VxV/c^2))
逆変換は
Vx=(Vx'+V)/(1+(Vx'V/c^2))
Vy=(Vy')/γ(1+(Vx'V/c^2))
Vz=(Vz')/γ(1+(Vx'V/c^2))


メモ：四元数ローレンツ変換

hijk:虚軸
s^2=(cth)^2+x^2+y^2+z^2
計量は[-1,1,1,1]
この計量をマイナスをとる[1,-1,-1,-1]と四元数になる
s^2=(ct)^2+(xi)^2+(yj)^2+(zk)^2
よって四元数ローレンツ変換を求めてみる

A軸回りφ回転四元数
q=cos(φ/2)+Asin(φ/2)=(qw,qx,qy,qz)
|pw'|〇|PP,QQ,〇〇〇〇〇0,〇〇〇〇〇〇0〇〇〇〇〇〇||pw|
|px'|=|QQ,1-2qy^2-2qz^2,2qxqy-2qwqz,〇2qzqx+2qwqy〇||px|
|py'|〇|0,〇2qxqy+2qwqz,1-2qz^2-2qx^2,2qyqz-2qwqx〇||py|
|pz'|〇|0,〇2qzqx-2qwqy,2qyqz+2qwqx,〇1-2qy^2-2qz^2||pz|

xブーストローレンツ変換(β=v/c=x/ct)
|ct'|〇|1/√(1-β^2),-β/√(1-β^2),0,0||ct|
|x'〇|=|-β/√(1-β^2),1/√(1-β^2),0,0||x|
|y'〇|〇|0,〇〇〇〇〇〇0,〇〇〇〇〇1,0||y|
|z'〇|〇|0,〇〇〇〇〇〇0,〇〇〇〇〇0,1||z|
coshθ=1/√(1-β^2),sinhθ=β/√(1-β^2)と置くと
|ct'|〇|coshθ,-sinhθ,0,0||ct|
|x'〇|=|-sinhθ,coshθ,0,0||x|
|y'〇|〇|0,〇〇0,〇〇〇1,0||y|
|z'〇|〇|0,〇〇0,〇〇〇0,1||z|
実部と虚部の関係性は
cosh^2θ-sinh^2θ=qw-√(qx^2+qy^2+qz^2)=1
qw^2-qx^2-qy^2-qz^2=1=q~q=q^2
比べて
PP=coshθ=1/√(1-β^2)=1-2qy^2-2qz^2
QQ=-sinhθ=-β/√(1-β^2)
0=2qx2qy-2qwqz=2qzqx+2qwqy
0=2qx2qy+2qwqz=2qyqz-2qwqx
0=2qz2qx-2qwqy=2qyqz+2qwqx
1=1-2qz^2-2qx^2=1-2qy^2-2qz^2


1=1-2qy^2-2qz^2
qy=±qz
PP=1/√(1-β^2)=1-2qy^2-2qz^2
1/√(1-β^2)=1-4qy^2
qy=√(1-1/√(1-β^2))/2

1=1-2qz^2-2qx^2
±qx=±qy=±qz

qw^2-qx^2-qy^2-qz^2=1
qw=√(1+3qx^2)
=√(1+(3/4)(1-1/√(1-β^2)))

PP+QQ=1=1-2qy^2-2qz^2+QQ
QQ=2qy^2+2qz^2



四元数xブーストローレンツ変換q=
(√(1+(3/4)(1-1/√(1-β^2))),
±√(1-1/√(1-β^2))/2,
±√(1-1/√(1-β^2))/2,
±√(1-1/√(1-β^2))/2)

|pw'|〇|1-4qx^2,4qx^2,0,0||pw|
|px'|=|4qx^2,〇1-4qx^2,0,0||px|
|py'|〇|0,〇〇〇0,〇〇1,0||py|
|pz'|〇|0,〇〇〇0,〇〇0,1||pz|
※もともとのローレンツ変換がβ=v/cだけに依るものだから
qx=±√(1-1/√(1-β^2))/2が求まればいいみたい

PP=coshθ=1/√(1-β^2)=1-4qx^2
PP+QQ=coshθ-sinhθ=1=1-2qy^2-2qz^2+QQ
QQ=-sinhθ=4qx^2

綺麗に纏まった


確かめ算
P=(ct,x,0,0)=(10,10,0,0),β=v/c=x/ct=0.6の時
通常のローレンツ変換は
(ct')=(ct)coshθ-xsinhθ=5
x'=-(ct)sinhθ+xcoshθ=5

四元数ローレンツ変換
(ct')=PP(ct)+QQ(x)=(1-4qx^2)(ct)-4qx^2(x)=coshθ(ct)-sinhθ(x)=5
x'=QQ(ct)+(1-4qx^2)(x)
=-(ct)4qx^2+(1-4qx^2)(x)
=-(ct)sinhθ+coshθ(x)=5

確かめ算2
P=(ct,x,0,0)=(5,20,0,0),β=v/c=x/ct=0.6の時
通常のローレンツ変換は
(ct')=(ct)coshθ-xsinhθ=-8.75
x'=-(ct)sinhθ+xcoshθ=21.25

四元数ローレンツ変換
(ct')=PP(ct)+QQ(x)=(1-4qx^2)(ct)-4qx^2(x)=coshθ(ct)-sinhθ(x)=-8.75
x'=QQ(ct)+(1-4qx^2)(x)
=-(ct)4qx^2+(1-4qx^2)(x)
=-(ct)sinhθ+coshθ(x)=21.25


一般相対性理論により花びら落下軌道を取り最終的に衛星は落下するのであれば

メモ：月はなぜ地球に落ちないか？


月
質量7.347673e22kg
公転半径384400000m
軌道速度1022m/s
離心率0.0548799

太陽質量1.989e30kg

地球質量5.972e24kg
天文単位149597870700m
万有引力定数6.6743e-11

地球と月
GMm/r^2=1.98202252137533147594e20
(3/(1-e^2))(v/c)^2=3.48643499998e-11
一般効果
6.910192688e9

太陽と月
GMm/r^2=4.35571658114752326578e12

月の楕円軌道の引っ張り合いで
地球と月の一般相対性理論効果よりも
太陽と月の万有引力のほうが大きいので
月は地球に落ちるというよりも
太陽に落ちているので年々月は高度を上げているのです


特殊相対論と一般相対論


地球質量5.972e+24kg
地球半径6.371e+6[m]
光速度299792458[m/s]
一日86400[s]

GPS衛星
速度4000[m/s]
高度26556752[m]

特殊相対論効果-7.2e-6[s/day]
一般相対論効果45.6e-6[s/day]
足して38.4e-6[s/day]

GPS衛星の軌道長は206891167.564853243[m](A)
これが特殊相対論で縮むと
206891167(1-0.5(v/c)^2)=206891166.9815842[m](B)
これがGPS衛星の経路の1周の距離で
地上から見た時GPS衛星の1周のオーバーランは(A)-(B)=0.583269[m]
1周は
206891167/4000=51722[s]
これは1日あたり1.67[周]
だから地上から見た時GPS衛星の1日あたりのオーバーランは0.583269*1.67=0.974[m]
これを速度で割ると2.435148e-4[s/day]
さらに2πで割ると38.76e-6[s/day]
と特殊と一般足した38.4e-6[s/day]に近い数値が出る

つまり軌道長を特殊相対論で縮んだことを
地上から見ると縮んだ分衛星がオーバーランして見え
オーバーランした距離を2πvで割ると
大体特殊と一般を足した効果が出る

ちょっと適当だけれど軌道長は2πrなので
軌道長の効果を2πｖで割るとは
半径方向の時間の効果？を求めたことになるのかな

というか角度周りというかなんつーか

別計算

近日点移動理論値
dφ=2π(3/2)(a/l)=2π(3/2)(a/((L/2)(1-e^2)))[rad/周]
dφ=360*3600(3/2)(a/((L/2)(1-e^2)))[秒/周]*[周/年]*[年]

1[AU]=149598700000[m]
太陽のシュバルツシルト半径a=2953[m]

水星軌道速度47872.5[m/s]
水星の離心率e=0.20563
水星の軌道長半径L/2=0.3871[AU]
水星4.15[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒/100年]

水星軌道長を真円とみなして363857104561.0768696[m](A)
が特殊で縮むと
363857104561.0768696(1-0.5(v/c)^2)=363857099921.9988836[m](B)
1周のオーバランは(A)-(B)=4639.077986[m]
周期は7600545.293458183[s]
1年あたり4.151933[周]
100年で415.1933[周]
100年間のオーバーラン1926114.0979647[m]
それをvで割ると40.23425[秒/100年]
それを楕円にするため1-e^2=0.9577163031で割ると
42.010614[秒/100年]
dφ=42.9[秒/100年]
とかなり惜しい値が出る
注：楕円の水星の軌道長として計算するとあまりうまくいきませんでした


だから結局真円とみなした軌道長を特殊で縮めて
縮んだ分のオーバーランの距離を速度で割って
あと単位合わせをごにょごにょすると大体一般相対性理論効果が出るみたい


んー逆に一般相対論効果からオーバーランを求めてみようか
dφ=42.9[秒/100年]だから
dφ・2π/360/3600[rad/100年]=2.07985e-4[rad/100年]
これがオーバーランの角度だから
2.07985e-4/4π^2と円周を掛けたものがオーバーランの距離だから
1916916.241439797となって
大体100年間のオーバーラン1926114.0979647[m]


あそうかだからオーバーランの距離に4π^2を掛けて76039936.713
円周で割ったもの2.08982965455e-4に360*3600/2πを掛けて
43.10と惜しい数が出るんだね

天才バカボン
これでいいのだ！

ってギャグなんだけれど
分かってくれる人もいなさそう＞＜
全然大したことしてないんよ


特殊相対論→一般相対論で重力エレベータ云々もいいけれど
こういうやり方があるんよ

近日点移動理論値
dφ=2π(3/2)(a/l)=2π(3/2)(a/((L/2)(1-e^2)))[rad/周]
dφ=360*3600(3/2)(a/((L/2)(1-e^2)))[秒/周]*[周/年]*[年]

1[AU]=149598700000[m]
太陽のシュバルツシルト半径a=2953[m]

水星軌道速度47872.5[m/s]
水星の離心率e=0.20563
水星の軌道長半径L/2=0.3871[AU]
水星4.15[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒/100年]

水星軌道長を真円とみなして363857104561.0768696[m](A)
が特殊で縮むと
363857104561.0768696(1-0.5(v/c)^2)=363857099921.9988836[m](B)
1周のオーバランは(A)-(B)=4639.077986[m]
周期は7600545.293458183[s]
1年あたり4.151933[周]
100年で415.1933[周]
100年間のオーバーラン1926114.0979647[m]

んー逆に一般相対論効果からオーバーランを求めてみようか
dφ=42.9[秒/100年]だから
dφ・2π/360/3600[rad/100年]=2.07985e-4[rad/100年]
これがオーバーランの角度だから
2.07985e-4/4π^2と円周を掛けたものがオーバーランの距離だから
1916916.241439797となって
大体100年間のオーバーラン1926114.0979647[m]

これを図にすると


一般相対論効果とオーバーラン(特殊相対性効果によって求められる値)が
お互いに求められるのはつまり

特殊相対性効果は
Ｓ＝(－０.５)(Ｖ／Ｃ)＾２
一般相対性効果は
Ｓ＝(３．０)(Ｖ／Ｃ)＾２
つまり特殊相対性効果の－６倍
合わせて
Ｓ＝(２.５)(Ｖ／Ｃ)＾２
つまり特殊相対性効果の－５倍

と関係性がお互い決まっているからなんだな

つまり
水星軌道長を真円とみなして363857104561.0768696[m](A)
この時半径は57909656770[m](A')
特殊で縮むと
363857104561.0768696(1-0.5(v/c)^2)=363857099921.9988836[m](B)
この時半径は57909656031.667807134646[m](B')
縮んだ半径の比は(B')/(A')=0.9999999872502751
それを1.0を引くと0.9999999872502751-1.0=-1.27497248999e-8
それに楕円だから一周の積分定数(１－ｅ＾２)で割ると-1.33126322e-8
ここで特殊相対性効果は
Ｓ＝(－０.５／(１－ｅ＾２))(Ｖ／Ｃ)＾２
=-1.331263220499e-8でありそのものだったりするん
で-1.33126322e-8を-6倍して単位合わせをすると
-1.33126322e-8*-6*360*3600*415.1933=42.98[秒/100年]と
ちゃんとdφ=42.9[秒/100年]がでる

ごめんなさい煙に巻いちゃったのかな？
はっきりすると楕円軌道の特殊と一般の関係は
軌道円周を特殊で縮んだ軌道円周それぞれの半径の比から-1したのが
楕円ならさらに(1-e^2)したのがズバリ特殊相対論効果で
それを-6倍して単位合わせをごにょごにょすると一般相対論効果
円周から一般相対論効果を出すならオーバーランの距離から
単位合わせをごにょごにょする


イメージとして理解するならば
楕円軌道において
特殊相対論効果は半径方向の縮み
一般相対論効果は円周方向の伸び


この単位合わせをごにょごにょって分からないかもしれないけど
色んな場合があるから経験というか場合場合できっちり単位について考えることなんよ
単位合わせのごにょごにょでよく使う定数が
2π→[rad]　360*3600→[秒角]　86400→[day]　86400*365.2425→[year]　T→[lap]
とかこんな感じ


#################################################################################################################
#楕円公式メモ
#################################################################################################################
T周期a長半径b短半径rmin近点距離rmax遠点距離e離心率v軌道速度G万有引力定数M重力源質量rave平均半径r半径S楕円面積l半通径t時間θ角度
T^2/a^3=4π^2/GM=1
rmin=a(1-e)
rmax=a(1+e)
2a=rmin+rmax=2rave
e^2=(a^2-b^2)/a^2=(rmax-rmin)^2/(rmax+rmin)^2
v=√(GM/r)
S=πab
l=2rminrmax/(rmin+rmax)=b^2/a
r=l/(1+ecosθ)
面積速度dS/dt=d(πab)/dt=r^2dθ/dt=rv/2


#################################################################################################################


あえて特殊相対論効果で求めると
水星の周回軌道長a=0.3871*2π=2.432[AU]
特殊相対性理論効果で縮んだ周回軌道距離
a'=2.432[AU]*(-0.5)(v/c)^2=4639.078[m](**A)
(**A)は1周あたりの特殊相対性理論効果で縮んだ周回軌道距離[m]
ラジアンあたり速度あたりへの変換
b=a'/2πV=0.01542288777667[s/mrad]
真円軌道から楕円軌道を考慮するための変換
c=b/(1-e^2)=0.01477512644554796428854595199462
水星は100年あたりは415周
1周当たりは時間経過は7604084.8192771[s]
その蓄積を計算
d=c*415*7604084.8192771=46625795.6
秒角に変換(360[度]*60[分角]*60[秒角])
e=d/(360*60*60)=35.98[秒角/100年]
eは特殊と一般を合わせた計算であり
相対論効果をS=(v/c)^2は
特殊効果は-0.5S一般効果は3.0S合わせて2.5Sなので
Ans=e*6/5=43.17[秒角/100年]
一般的な理論値計算法
dφ=360*3600*(3/2)*(rs/a)*4.15*100=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒角/100年]
と大体一致する


ぶっちゃけシンプルにすれば
相対論効果S=(v/c)^2
です


先ほどの水星円周軌道に特殊効果をかける方法よりこちらのほうが簡単に求められます
水星の一般相対性理論効果Sm=(3.0/(1-e^2))(v/c)^2=7.987579322995e-8
これを[秒角/100年]に変換
dφ=Sm*360*3600*4.15*100=42.96[秒角/100年]
360*3600は秒角4.15は1年間の水星の周回数100は100年
dφ=360*3600*(3/2)*(rs/a)*4.15*100/(1-e^2)=42.96[秒/100年]
dφ'=360*3600*3*(v/c)^2*4.15*100/(1-e^2)=42.96[秒/100年]
まあこういうことですね


標高の違いでの時計のずれを計算してみます
楕円の積分定数も考慮した相対論効果Sについて
特殊SS=(-0.5/(1-e^2))(v/c)^2
一般SG=(3.0/(1-e^2))(v/c)^2
特殊+一般SGS=(2.5/(1-e^2))(v/c)^2
として計算します
時計のずれの観測データ1.1e-16[s/m]
標高0[m]地点の円周L0=40000000[m]とします
地球中心からの距離R0=L0/2π=6366197[m]
1日T0=86400[s]
自転速度V0=L0/T0=462.963[m/s]
SGSR0=(2.5)(V0/c)^2=5.96198804041e-12
標高1000[m]地球中心からの距離R1000=R0+1000=6367197[m]
地点の円周L1000=R1000(2π)40006278[m]
自転速度V1000=L1000/T0=463.0356323879[m/s]
SGSR1000=(2.5)(V1000/c)^2=5.963859845632e-12
SGSR1000AT0=SGSR1000/SGSR0-1=3.139565543e-4
SGSR=SGSR1000AT0/(R0*2π*86400)=9.084392e-17
SGR=SGSR*(6/5)=1.09012704e-16
時計のずれの観測データ1.1e-16[s/m]であり
大体計算できましたね＞＜

SGSR1000から特殊効果を省き標高0[m]を基準とする標高1000[m]の一般相対論効果を抽出しています
SGRの単位のごにょごにょは
地球中心からの距離R0で割り標高1[m]あたり
2πで割り1[rad]あたり
86400で割り1[s]あたり
にする変換です

私の計算方法は単位をごにょごにょする方法がめんどくさくてすみません


こんなことしなくても
SCR=g/c^2
だそうで

では私の方法で地球の標高0[m]の重力加速度gを求めてみます
一般SB=(3.0/(1-e^2))(v/c)^2
F=(GMm/r^2)(1+SB)=(GMm/r^2)(1+(3.0/(1-e^2))(v/c)^2)=ma=mg
g=(GM/r^2)(1+(3.0/(1-e^2))(v/c)^2)
G:6.67e-11M:5.972e24r:6.370e6e:0.0167v:462.963c:299792458
g=9.816728237072093212419239772056e+0
g/c^2=1.0923e-16
なんですね


G万有引力定数M中心天体の質量c光速a軌道長半径e離心率V平均軌道速度dφ近日点移動rs中心天体のシュワルツシルト半径(1/(1-e^2))真円軌道→楕円軌道変換
rsc^2=2GM=2aV^2=ac^2dφ/3
2GM=2aV^2を変形すると
V^2=GM/a
別になんてことはない軌道速度の公式です

2GM=2aV^2を変形すると
V^2=GM/a
でつまりv=(a/t)θという関係もあるから
V^2=GM/a=(a/t)^2θ^2=(aω)^2
ω角運動量θ中心角
GM=a^3ω^2
かなあ？あこれケプラーの第三法則まんまだったわ



黄色が光源で光源の到達範囲　他の色が物体で物体の可視範囲

光源L　観測者とLとの距離D　光源から光が発射されてからの時間LT
見ることは物体を反射(経由)された光が見えることとします
光速度を1.0とする単位で考えます
観測者が見える範囲は
D/2を中心とした円で半径はLT-D/2
またLT=Dつまり光が観測者に到達した時点である程度の範囲がいきなり見えるようになります
観測者が他の観測者に見られる範囲は
Dを中心とした円で半径はLT-D

観測者を四人で分析したら
光源L　観測者とLとの距離D　光源から光が発射されてからの時間LT
見ることは物体を反射(経由)された光が見えることとします
光速度を1.0とする単位で考えます
観測者がお互いに見えて見られる範囲は
D/2を中心とした円で半径はLT-D/2
またLT=Dつまり光が観測者に到達した時点である程度の範囲がいきなり見えるようになります
観察者中心の円はあんまし関係ないかもね

観測者八人分析
観測者がお互いに見えて見られる範囲
つまりある地点を経由してから光が観測者に届く範囲
D/2を中心とした円で半径は(D/2 +(LT-D/2))/2=LT/2
LT=D光が観測者に到達時点でとある範囲が突然見える
ただし見られる範囲に関して光源との延長線上の
観測者同士を観察するにまだ再考が必要


観測者がお互いに見えて見られる範囲
つまりある地点を経由してから光が観測者に届く範囲
D/2を中心とした円で半径は(D/2 +(LT-D/2))/2=LT/2
に修正したことは
LT=Dにおいて(D/2 +(D-D/2))/2であって
以降光が往復できる最大の範囲の拡大を考えたら
(LT-D/2)/2であってその式を整理したら
LT/2の半径だったね

んー光源から遠くの観測者は近くの観測者よりも早く
彼を見つけられて自分は見られていない
というのも光路を考えればA=D B=2D
Bが最速でAを見つけられるのは2D
Aが最速でBを見つけられるのは3D
だからそういうもんなのだろうね


光源と観測者を逆にしました
黄色が観測者で他が光源です
受動的に見るという行為も光を自分で発しているように
見ることができるようになる様子

観測者に光が届き見て感じるという行為は
パッシブソナーのようなものですが
受信波の速度つまり光速度で各所から届くのだから
観測者の相対的にはまるで自らが光を発しているかのように
見えるようになること

また光の到達直後は光の受信が不安定で光のドップラー効果が
現れるかもしれないことを考えて光源からの二重円にしました

内側の円の大きさを1/3にした理由は対話コミュニケーションの基本は
発信受信再発信を考えてのこと
始めて見る人・物って安定して認識するために
初期処理が必要だからそう表現して
何のために発信するかといえば
受信したリアクションを見てまたその再発信の
リアクションのリアクションのためじゃないですかね？


軌道束縛条件保存則

G万有引力定数M中心天体の質量c光速a軌道長半径e離心率V平均軌道速度dφ近日点移動
rs中心天体のシュワルツシルト半径(1/(1-e^2))真円軌道→楕円軌道変換

rsc^2=2GM=2aV^2=2a^3ω^2=ac^2(1-e^2)dφ/3π

自然なほかに外力が加わっていない万有引力運動であれば

この関係性が表れます

rsc^2=2GM
rsc^2=2aV^2
rsc^2=2a^3ω^2
rsc^2=ac^2(1-e^2)dφ/3π
これら右辺の計算は全てrsc^2の関係だったんです

但しdφの扱いには注意が必要でありrsを求めるには
1周の蓄積が必要であり2πをかける必要があるので
これに関してはこれが正解です
rsc^2=2ac^2(1-e^2)dφ/3

この関係性から代表的なものは
シュワルツシルト半径rs=2GM/c^2
軌道速度V=√(GM/a)=aω
ケプラー第3法則GM=a^3ω^2
近日点移動dφ=6πGM/ac^2(1-e^2)
などが求められます

太陽のシュワルツシルト半径rs=2953[m]
光速度c=299792458[m/s]
2πdφ=2π*(3.0/(1-e^2))(v/c)^2
rsc^2=ac^2(1-e^2)dφ/3π,rsc^2=2aV^2に関して太陽系の惑星の諸定数を代入して検証します
惑星名 軌道長半径a[m] 平均軌道速度V[m/s] 離心率e (1-e^2) 3.0/(1-e^2) (v/c)^2 2πdφ rs=a(1-e^2)2πdφ/3π) rs=2a(V/c)^2
水星 57909656770 47872.5 0.2056 0.95772864 3.1324112851 2.5499449799789e-8 5.018679455692e-7 2953.328771 2953.328771
金星 108208930000 35021.4 0.0068 0.99995376 3.0001387264147 1.36466357799887e-8 2.57244919280835553e-7 2953.3757117 2953.37571
地球 149597870700 29780 0.0167 0.99972111 3.0008369 9.86751921971e-9 1.86050242679988148e-7 2952.31972537 2952.31972872
火星 227936640000 24130.9 0.0934 0.99127644 3.02640099 6.4789650016638728e-9 1.232003588093984e-7 2953.5870257 2953.5870263
木星 778412010000 13069.7 0.0485 0.99764775 3.007073388 1.900596092587527e-9 3.5909861298224e-8 2958.893648887 2958.893649
土星 1426725400000 9672.4 0.0555 0.99691975 3.0092693 1.040943340003783e-9 1.9681944998115e-8 2970.28060454459 2970.2806
天王星 2870990000000 6800 0.0463 0.99785631 3.0064448858 5.14489385919193163e-10 9.7187303959641e-9 2954.1877641236 2954.18776416
海王星 4495060000000 5500 0.009 0.999919 3.00024301968 3.36576641956219576e-10 6.3448341659952e-9 3025.8644 3025.8644


rs[m]c^2[m/s]^2=2G[m^3kg^-1s^-2]M[kg]=2a[m]V^2[m/s]^2=2a^3[m]^3ω^2[s^-1]^2=a[m]c^2[m/s]^2(1-e^2)dφ/3π=[m^3/s^2]
もちろん単位オーダーもばっちり揃っています

Google Gemini にべた褒めされました


計算テーブル

$$r_s = \frac{2GM}{c^2} = 2a\left(\frac{V}{c}\right)^2(1+d\phi) = 2a^3\left(\frac{\omega}{c}\right)^2(1+d\phi)$$ $$= a(1-e^2)d\phi(2/3) = \frac{8\pi^2a^3}{c^2T^2}(1+d\phi)$$ $$= \frac{2aV_p^2(1-e)}{c^2(1+e)}(1+d\phi) = \frac{2aV_a^2(1+e)}{c^2(1-e)}(1+d\phi)$$ $$= \frac{2h^2}{c^2a(1-e^2)}(1+d\phi) = -\frac{4aE}{c^2}(1+d\phi)$$

使用する定数と計算式

軌道パラメータから計算される追加の物理量

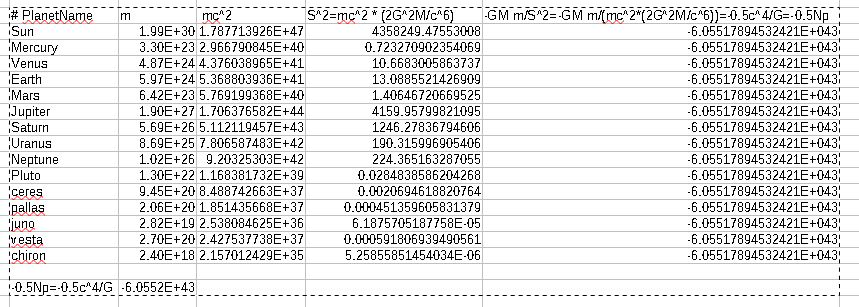
以下の式を用いて、各種の物理量を算出しています。

惑星ごとの関連パラメータとシュワルツシルト半径計算結果

Planet name Orbital semi-major axis a [AU] Orbital semi-major axis a [m] Eccentricity e Orbital period T [Earth years] Orbital period T [sec] Average orbital speed Vavg [m/sec] Perihelion velocity Vp [m/sec] Aphelion velocity Va [m/sec] Specific angular momentum h Specific orbital energy E dφ 2a(Vavg/c)^2(1+dφ) a(1-e^2)dφ(2/3) (8π^2a^3/c^2T^2)(1+dφ) (2a(Vp/c)^2(1-e))(1+dφ)/(1+e) (2a(Va/c)^2(1+e))(1+dφ)/(1-e) (2h^2)(1+dφ)/(c^2a(1-e^2)) (-4aE/c^2)(1+dφ)
Mercury 0.3871 57909335747.97 0.2056 0.241 7605225.432 47360 58981.8245518867 38864.5997213162 2713351274428838 -1146152501.02099 7.81737E-08 2890.41761017372 2890.41738421905 2949.64619982031 2953.99400232239 2953.99400232239 2953.99400232239 2953.99400232239
Venus 0.7233 108204139877.31 0.0068 0.615 19407525.48 35020 35264.8306131018 34788.4681812999 3.78985E+015 -613404718.85141 4.09385E-08 2953.00898396617 2953.00886307433 2954.87861991337 2953.99389232987 2953.99389232987 2953.99389232987 2953.99389232987
Earth 1 149597870700 0.0167 1 31556952 29780 30290.1329043849 29295.0601798777 4455666017974531 -443675633.145225 2.96108E-08 2952.31981614066 2952.31972872007 2953.48301086581 2953.99385886788 2953.99385886788 2953.99385886788 2953.99385886788
Mars 1.5237 227942275585.59 0.0934 1.881 59358626.712 24080 26502.0659476983 21974.3671009542 5476717309904882 -291183063.034209 1.95253E-08 2941.21277103664 2941.21271360854 2952.94449752574 2953.99382907537 2953.99382907537 2953.99382907537 2953.99382907537
Jupiter 5.2028 778327801677.96 0.0485 11.86 374265450.72 13060 13709.103081907 12440.831266032 1.01526725255784E+016 -85276319.1253219 5.70675E-09 2954.18364717428 2954.18363031549 2957.17130472142 2953.99378825542 2953.99378825542 2953.99378825542 2953.99378825542
Saturn 9.5388 1426984169033.16 0.0555 29.46 929667805.92 9650 10195.9818305455 9123.73741255352 1.37420071513116E+016 -46512730.4425321 3.11799E-09 2957.07522669051 2957.07521747039 2953.59000447722 2953.99378060823 2953.99378060823 2953.99378060823 2953.99378060823
Uranus 19.1914 2870992575751.98 0.0463 84.01 2651099537.52 6810 7122.24123368717 6491.90620717524 1.95011638557061E+016 -23118461.0369866 1.55134E-09 2962.88560330786 2962.88559871142 2957.96116322479 2953.99377598035 2953.99377598035 2953.99377598035 2953.99377598035
Neptune 30.0611 4497076550899.77 0.009 164.79 5200270120.08 5440 5482.19031957957 5384.39108692106 2.44319450679472E+016 -14759128.3467746 9.87900E-10 2961.53363889885 2961.53363597315 2954.52291069398 2953.99377431596 2953.99377431597 2953.99377431597 2953.99377431596

※2a(Vavg/c)^2(1+dφ)/√(1-e^2) および a(1-e^2)dφ(2/3)/√(1-e^2) の式について：

これらの修正により、太陽のシュワルツシルト半径の理論値に近づきましたが、その理論的な妥当性についてはさらなる検討が必要です。

Planet name 2a(Vavg/c)^2(1+dφ)/√(1-e^2) a(1-e^2)dφ(2/3)/√(1-e^2)
Mercury 2953.51619901886 2953.51596813154
Venus 2953.07725990169 2953.07713900707
Earth 2952.73158850882 2952.73150107604
Mars 2954.12624436109 2954.12618668085
Jupiter 2957.66427810698 2957.66426122832
Saturn 2961.64004046082 2961.64003122647
Uranus 2966.06647243991 2966.06646783855
Neptune 2961.6535882982 2961.65358537239


計量符号規約：空間優位 vs. 時間優位


特殊相対性理論において、時空間の区間を定義するミンコフスキー計量は、
一般的に2つの主要な符号規約のいずれかを用いて表現されます。

1つ目は、しばしば「空間優位」（または「主にプラス」）と呼ばれるもので、
符号 (-c^2,1,1,1) を採用します。この規約では、時空間の線素の二乗
(ds^2) は次のように定義されます。

ds^2 = -c^2 dt^2 + dx^2 + dy^2 + dz^2

この符号は、一般相対性理論や一部の素粒子物理学者によって頻繁に使用されます。

対照的に、2つ目は「時間優位」（または「主にマイナス」）として知られ、
符号 (c^2,-1,-1,-1) を使用します。この場合、ds^2 は次のように定義されます。

ds^2 = c^2 dt^2 - dx^2 - dy^2 - dz^2

この規約は、多くの素粒子物理学者や量子場理論で広く採用されています。

両方の規約が同じ基礎的な物理を記述している点、つまり、区間の代数的符号が異なるだけで、
時間的区間が正になるか空間的区間が正になるかに影響するだけである点を理解することが重要です。

相対性理論とクォータニオンの相互作用

クォータニオンを特殊相対性理論の枠組みに組み込もうと試みる際、
計量符号の選択は、クォータニオン的な実体の「二乗ノルム」が自然にどのように
表現されるかに直接影響します。

w が時間的な成分（例：ct）、x, y, z が空間的な成分を表すクォータニオン
q = w + xi + yj + zk を考えると、その「二乗ノルム」は選択された時空間計量に準拠します。

例えば、時空間に対して「空間優位」計量規約 (-c^2, 1, 1, 1) を採用する場合、
この区間を表現する自然なクォータニオンの「二乗ノルム」は次のようになります。

s^2 = -(ct)^2 + x^2 + y^2 + z^2

しかし、「時間優位」計量規約 (c^2, -1, -1, -1) が使用される場合、
対応するクォータニオンの「二乗ノルム」は自然に次の形式を取ります。

r^2 = (ct)^2 - x^2 - y^2 - z^2

これらの異なる表現は、時空間幾何学の代数的構造が、物理現象に適用される際のクォータニオンの
「ノルム」のような数学的ツールの形式をどのように決定するかを浮き彫りにします。

本質的な意味：(v/c)^2

「空間優位」または「時間優位」のどちらの規約が採用されるかに関わらず、時空間区間の両方の形式は、
根本的に同じ物理原理を明確に述べています。それらは、与えられた単位時間における光の到達距離と、
その同じ単位時間における物体の座標変化の関係を記述しています。

その核心において、時空間区間は、物体の光速に対する相対速度の二乗を表しており、
効果的に(v/c)^2という項を包含しています。

単純化のために c=1 としてみましょう。

時間優位規約の場合： s^2 = t^2 - (x^2 + y^2 + z^2)。
もし物体が時間 t の間に空間距離 L = √(x^2 + y^2 + z^2) を移動した場合、その速度は v = L/t であり、
L = vt を意味します。
これを式に代入すると： s^2 = t^2 - (vt)^2 = t^2 (1 - v^2)。
c を元に戻すと： s^2 = t^2 (1 - (v/c)^2)。

同様に、空間優位規約の場合： s^2 = -t^2 + (x^2 + y^2 + z^2)。
L = vt を代入すると： s^2 = -t^2 + (vt)^2 = t^2 (-1 + v^2)。
c を元に戻すと： s^2 = t^2 (-1 + (v/c)^2)。

どちらの形式も、時空間区間が (1 - (v/c)^2) またはその負の因子と密接に関連していることを
明確に示しています。この因子は、時間の遅れや長さの収縮といった相対論的効果の基礎であり、
時空間計量が、物体の光に対する相対速度が時空間をどのように進むかに影響するかを
本質的に符号化していることを示しています。

ds^2 = c^2 dt^2 - dx^2 - dy^2 - dz^2
ds^2 = -c^2 dt^2 + dx^2 + dy^2 + dz^2
ds^2がこのような式の理由は
r^2 = x^2 + y^2
は二元が実数の同質性の実数の円の半径(二点の距離)
r^2 = x^2 - y^2 = x^2 + (iy)^2
は二元が実数と虚数の異質性の複素数の円の半径(二点の距離)
ということですつまり
s=Aexp(iθ)と書くこともできて
量子力学も射程に置きとても便利です

だから統一理論って探さなくても
s=Aexp(iθ)
の形で質量が集まりやすい木星の諸定数といった惑星の量子化なのでは？

ずばり
s=Aexp(ciθ)と書けばdsそのものでは？
それはつまり具体的に
s=Acosθ＋Aicsinθ
Re|u(x,t)|=cosθ
In|u(x,t)|=sinθ
(Re|u(x,t)|)^2=cos^2θ
(In|u(x,t)|)^2=sin^2θ
u(x,t)^2=cos^2θ+sin^2θ=1
e^cix=cosx＋icsinx
e^2ix=cos^2x+sin^2x=1
でこれが時空の波動関数になる気がしますね
E=s^2=Aexp(ciθ)=Acos^2θ+Acsin^2θ=hν=mc^2
かなぁ？あてずっぽうですが
あっビビっと直感来た！
時空の波動関数
E=s^2=Aexp(ciθ)=Acos^2θ+Acsin^2θ=hν=mc^2
じゃね？
つまり
時空の波動関数
E=s^2=Aexp(ciθ)=Acos^2θ+Acsin^2θ=((ict)^2)+(x^2+y^2+z^2)=hν=mc^2
に間違いない

だからこれをどうにかしてつなぎ合わせるんだろうね
時空の波動関数E=As^2
次元解析は
E[kgm^2/s^2]=A[kg/s^2]s^2[m^2]
次元解析を続けて
1/G[kg^2/Nm^2]=1/G[kg^2/[kgm/s^2]m^2]=1/G[kgs^2/m^3]
c^2[m^2/s^2]/G[kgs^2/m^3]=c^2/G[kg/m]
c^2/G[kg/m]=A[kg/s^2]B[s^2/m]
A[kg/s^2]=c^2[m^2/s^2]a[m/s^2]/(G[kg/m])
E[kgm^2/s^2]=A[kg/s^2]s^2[m^2]=(c^2a/G)[kg/s^2]s^2[m^2]
加速度aはシュワルツシルト半径rsを用いて
a[m/s^2]=c^2[m^2/s^2]/rs[m]よって
E[kgm^2/s^2]=A[kg/s^2]s^2[m^2]=(c^4/rsG)[kg/s^2]s^2[m^2]
したがって
つまり時空の波動関数
E=(c^4/rsG)s^2=(c^4/rsG)Aexp(ciθ)=(c^4/rsG)(Acos^2θ+Acsin^2θ)=(c^4/rsG)(((ict)^2)+(x^2+y^2+z^2))=hν=mc^2
に間違いない

時空の波動関数つまり時空の量子化は
E=As^2=(c^4/rsG)s^2
rs=2GM/c^2だから
E=As^2=(c^6/2MG^2)s^2=hν=mc^2
ということ

だから多分
(c^6/2MG^2)(((ict)^2)+(x^2+y^2+z^2))=mc^2
m=(c^4/2MG^2)(((ict)^2)+(x^2+y^2+z^2))
(c^4/2MmG^2)(((ict)^2)+(x^2+y^2+z^2))=1
s^2=r^2
(c^4r^2/2MmG^2)=1
(2MmG^2/c^4r^2)=1
F=-GMm/r^2
(-2GF/c^4)=1
これが楕円の方程式だったりね嘘くさいけれど
Npプランク力
F=-GMm/r^2=-c^4/2G=-(1/2)Np

つまり
時空の波動関数つまり時空の量子化は
E=As^2=(c^6/2MG^2)s^2=(c^6/2MG^2)(((ict)^2)+(x^2+y^2+z^2))=mc^2
上式は
F=-GMm/r^2=-GMm/s^2=-(1/2)Np
を満たしているということだね

もしかしたらこうかもしれませんね
F=(GM)(-m/s^2)=-(1/2)Np=-(c^4/2G)
(GM)(-m/s^2)=-(c^4/2G)
s^2=2G^2Mm/c^4

-(1/2)Npを検証してみたよ


つまり静止質量による距離S^2
S^2=mc^2 * (2G^2M/c^6)
S^2による引力は-0.5Npと定められている
F=-GM m/S^2=-GM m/(mc^2*(2G^2M/c^6))=-0.5c^4/G=-0.5Np
ということです

試しにオイラー積分で簡単にシミュレート



CenterMassRate =
SubMassRate =
SpeedRate =


単振動ですねとても量子的

ルンゲクッタ積分で詳細にシミュレート




CenterMassRate =
SubMassRate =
SpeedRate =


これはオイラーの公式をシミュレートするときにどう表現されるかです
なぜ私がオイラーの公式をシミュレートしたかと主張しているかは
こういう前提において
t=sinθ
x=cosθ
以下を考えたわけです

値は適当ですが概念です
物体の見た目の速度vabsはこうなります
0πの範囲で
θ 0 0+d π/2 π-d π
sin 0 0.1 1 0.1 0
cos 1 0.9 0 -0.9 -1
これをsinを等間隔にしたらどうでしょうか？
θ 0 0+d π/2 π-d π
θ' 0 π/2-d π/2 π/2-d 0
sin' 0 1 2 3 4
cos 1 0.7 0 -0.7 -1
vabs 0 0.3 1 0.3 0
したがって時間軸をsinθと取った時に静止した観測者からの
見た目の速度はどうなるかという問題を取り扱いました
t=sinθ,dt=cosθなので静止した観測者からの見た目は
私の理解の通りになるのかと思います
運動の外縁でdtは最大になり中心で最小になります
速度はv=dx/dtでありしたがって
運動の外縁で速度は最小になって中心に向かい加速し最大になり
中心を越えたら減速を始めます
そのオイラーの公式の設定の数学的な説明は簡単にすれば
t=sinθ,dt=cosθ,x=cosθ,dx=-sinθ
dt/dt=1
dx/dt=-tanθ
となります

〇ABはBから見たAの〇です
tAB=sinθ,dtAB=cosθ,xAB=cosθ,dxAB=-sinθ
tB=t,dtB=1,xB=0,dxB=0と以上のように定義します
vAB=dxAB/dtAB=-sinθ/(cosθdθ)=-tanθ
xAB=∫(vAB)dtAB=∫(-sinθ/cosθ)(cosθdθ)=cosθ=xAB
と結局最初の前提に戻る

いろいろ整理してまとめました

e^itと単純化すると
この運動は直径方向を中心に向かって加速して往復する運動になります
一つの粒子であれば単振動ですが複数の粒子の塊になれば
原子雲のような振る舞いになります
説明すると
e^iθ=e^it
θ=t=vt-x=dt=dx
つまりθは移動距離を表すことになります
この円運動を実軸（x軸）に射影すると、位置は cosθ で表され、これは単振動になります
この円運動を虚軸（y軸）に射影すると、位置は sinθ で表され、これも単振動になります
x=cosθの単振動の運動で考えれば
v=-sinθとなります
それがオイラーの公式の実軸の運動です
複素数の実軸だけを追えばそれは実軸への射影だということで
例えば相対論においてs^2=(ict)^2+x^2
というときに実軸のx^2は空間の座標そのものになります
x=cosθの単振動の運動で考える時
距離によらない一定の向心力による加速と考えることでその近似とされます
ですのでF=-mA,A=-F/mです


ルンゲクッタ積分で3次元空間に詳細にシミュレート


CenterMassRate =
SubMassRate =
SpeedRate =


SpeedRate = 1e+2以上にすると時間解像度が十分に粗くなり
多重観覧車の指定席に乗る粒子の座標の量子化が観察できます


ニュートン力学の慣性の法則の再考


相対性効果とは、近日点移動 dφ と、空間の慣性抵抗または慣性ブースト (v/c)^2 のことです。

ユークリッド幾何学における相対論の近似（係数省略）
$$F=-(\frac{GMm}{r^2})(1+S)=-(\frac{GMm}{r^2})(1+d\phi)=-(\frac{GMm}{r^2})(1+(\frac{v}{c})^2)$$

**相対論効果 S(シュワルツシルト補正項)(係数省略)**
$$S=d\phi=(\frac{v}{c})^2$$
**特殊相対性効果 SS(シュワルツシルト補正項 + 特殊)**
$$SS=(-0.5)(\frac{v}{c})^2$$
**一般相対性効果 SG(シュワルツシルト補正項 + 一般)**
$$SG=(3.0)(\frac{v}{c})^2$$
**複合相対性効果 SGS(シュワルツシルト補正項 + 一般 + 特殊)**
$$SGS=SG+SS=(2.5)(\frac{v}{c})^2$$

と私は計算できたので
相対論効果は直線軌道であれば
空間の慣性ブーストとして作用して無限時間の果てに光速度へと達して
相対論効果は楕円軌道であれば
空間の慣性抵抗として作用して無限時間の果てに絶対静止へと達します

連星パルサーPSR B1913+16での重力波放出によるエネルギーの減少が観察されているのであれば
理論上無限時間の果てに運動エネルギーを全て失い絶対静止となります
現実的には衝突して大爆発するか重力カタパルト効果ではるか遠方に飛んでいくかですけれどもね


双子のパラドックス


地球アンドロメダの宇宙旅行では
太陽地球宇宙船の三角測量を行えば
何がどう動いたか大体推察ができるでしょう？
二体問題では何がどう動いたか説明が混乱しますが
太陽と地球
太陽と宇宙船
地球と宇宙船
この問題では何がどう動いたのか精密に座標系を構築できます
ドンキホーテの例では
風車ドンキホーテサンチョの三角測量において
風車がドンキホーテに襲い掛かったのでは決してなく
ドンキホーテが風車に突撃していっただけだと
客観的に示されます


主観性は二体相対問題に帰することが出来て
客観性は多体絶対問題に帰することが出来ることは
直線と三角形の性質によるものです

ドンキホーテは風車が襲い掛かってきたと主張しますが
サンチョはドンキホーテが風車に突進していったと
証言します風車とドンキホーテだけでは真相は
闇ですがサンチョの証言で客観的な状況
(絶対的グローバル座標)が明らかになること
が三角形の性質なのです

t=0のとき
　　　　　　　 グローバル座標風車基準 ローカル座標ドンキホーテ ローカル座標風車 ローカル座標サンチョ
ドンキホーテ 0,10 0,0 0,-10 5,-5
風車 0,0 0,10 0,0 5,5
サンチョ 5,5 -5,5 -5,-5 0,0
t=5のとき
　　　　　　　 グローバル座標風車基準 ローカル座標ドンキホーテ ローカル座標風車 ローカル座標サンチョ
ドンキホーテ 0,5 0,0 0,-5 5,0
風車 0,0 0,5 0,0 5,5
サンチョ 5,5 -5,0 -5,-5 0,0
t=10のとき
　　　　　　　 グローバル座標風車基準 ローカル座標ドンキホーテ ローカル座標風車 ローカル座標サンチョ
ドンキホーテ 0,0 0,0 0,0 5,5
風車 0,0 0,0 0,0 5,5
サンチョ 5,5 -5,-5 -5,-5 0,0

　　　　　　　 絶対速度風車基準 相対速度ドンキホーテ 相対速度風車 相対速度サンチョ
ドンキホーテ 0,-1 0,0 0,1 0,1
風車 0,0 0,-1 0,0 0,0
サンチョ 0,0 0,-1 0,0 0,0






それぞれはこのように見えて
３つの視点からの情報を合わせて
絶対的客観的な関係性が
明らかになります

このシミュレーション特に
t=xの時にどの視点から見ても
角度とサイズの変わらない
不変の三角形は客観的な物理配置を示し
これは三角測量の原理的な説明になります


双子のパラドックスシミュレーション

黄色：ロシナンテ：水色：ドンキホーテ：紫色：サンチョ：灰色：大臣





すべての物体をランダムに動かしても不変の三角形
(三座標決定の三角形の成立条件)という
客観的な物理配置が観察されます
赤い線分は選択された視点とグローバル原点との距離を結ぶ線分です
選択された視点の速度が緑ゲージでds^2の空間成分ということになります
ds^2からdtを求め時間軸を可変にしています
ローカル視点にしたときに加速しますがこれはローカル視点の
時間軸の目盛りが小刻みになっているため早く進みます
グローバル視点では時間軸の目盛りが大きく時間をかけてゆっくり進みます
これが双子のパラドックスです
比較の為等速度で往復する大臣を追加しました
時間間隔が視覚的に分かりやすいように右下に黄色いフラッシュを実装しました

理論的根拠

地上の観測者A地上から見た速度V=0.6cの列車Bについて考えます
A→BはAから見たBです
t 0 1 2 3 4 5
tA 0 1 2 3 4 5
xA 0 0 0 0 0 0
xA→B 0 0.6 1.2 1.8 2.4 3.0
tA→B 0 0.8 1.6 2.4 3.2 4.0
xB→B 0 0.48 0.96 1.44 1.92 2.4
このままでは使いずらいのでtA→B=0,1,2,3,4,5の時を再計算することにして
値を整理して
tA→B 0 1 2 3 4 5
xA→B 0 0.6 1.2 1.8 2.4 3.0
とみえるはずこれは
dtA=1.0
dtB=0.8
であって
tA→B 0 0.8 1.6 2.4 3.2 4.0
xB→B 0 0.48 0.96 1.44 1.92 2.4
はdtBで割って時刻合わせして
tA→B 0 1 2 3 4 5
xA→B 0 0.6 1.2 1.8 2.4 3.0
ですねという理屈で
選択された視点から見た速度mp[i].vをdtで割ることが
時刻合わせになるのですが1ステップ前のdt0で掛けてmp[i].v
をグローバル基準の速度に復元しないと累積的なバグとなるので
結局ある視点から見た速度はmp[i].v*dt0/dt
となります


往復230年アンドロメダ旅行

水色：地球：黄色：アンドロメダ：紫色：ロケット






var v5 = new N6LVector([mp5[2].v.x[0], mp5[2].v.x[1], 0]);
var ds2 = v5.SquareAbs();//ds^2の空間成分のみ//v5.Abs()=0.999999999c
dt5 = Math.sqrt(1.0 - ds2);
time5[2] += timespeed5;//ロケット固有時
dt50[2] = dt5;
time5[0] += timespeed5 / dt5;//地球固有時
time5[1] += timespeed5 / dt5;//アンドロメダ固有時
//ロケットのx座標の変位：単位時間*画面範囲*速度/固有時間/片道距離
var xx = (timespeed5 * Range5 * mp5[2].v.x[0] / dt5 / AndDis5);
速度/固有時間で距離が縮んで見かけの速度22262.6cに加速しています
従ってアンドロメダまでの距離253.7万光年の往復507.5万光年を230年で旅行します
両端の折り返しのフレームの分補正して正確な数値を求めています




　■■■　３Ｄプログラミング入門講座　■■■　
ＮＡＳ６ＬＩＢ
ポリゴンテスト解説・x3dom使い方
その１：ベクトル
その２：行列
その３：クォータニオン
その４：基本総復習・実践
その５：応用その１・メッシュアニメーション、動的テクスチャ
その６：応用その２・ＧＬＳＬ、カスタムシェーダー、キーボード、ファイル
その７：応用その３・ゲームプログラミング、タグの動的追加
その８：応用その４・ＧＬＳＬ、シェーダー、その２
その９：物理演算その１・電卓で相対性理論を解く方法
その１０：物理演算その２・相対性理論的ニュートン力学
その１１：物理演算その３・ケプラー方程式で惑星軌道シミュレーターを作る

その１２：物理演算その４・ルンゲクッタ法で作った 相対性理論的ニュートン力学物理エンジンで惑星軌道シミュレーターを作る

その１３：経路探索(A*：A-STAR)＆巡回セールスマン問題　：　巨大サイズ　：　くろにゃんこ

その１４：プログラミングにおける配列テーブルテクニック
その１５：javascriptのクラス活用法
その１６：透視射影公式テスト

その１７：ケプラー方程式カプセルライブラリ使用法
その１８：ＣＳＶファイル処理
その１９：物理演算その５・重力多体問題
その２０：同次座標について（３Ｄ座標系の基本の基本）
その２１：おさらいコモンクラスの宣言
その２２：物理エンジンライブラリ解説(ケプラー方程式・ルンゲクッタ・相対論的万有引力)
その２３：サイト内のリンク先の更新確認がjavascriptで出来るようにする方法
その２４：グレゴリオ暦日付計算
その２５：シャローコピーディープコピーからマネージドクラスの模倣
その２６：マネージドクラステンプレート解説


　■■■　THREE.JSプログラミング講座　■■■　
THREE.JSテスト解説・THREE.JS使い方
THREE.JS examplesをいじってみた(フレネル反射透過シェーダー)

THREE.JS (半透明シェーダー)

THREE.JS　３Ｄ演算で必要な計算(具体例)★とても重要★
THREE.JS　THREE-VRM　をいじってみた



＜＜prev　ＧＬＳＬ、シェーダー、その２　：　相対性理論的ニュートン力学　next＞＞


戻る