3Dプログラミング入門講座・その10:物理演算その2・相対性理論的ニュートン力学
電卓で相対性理論を解く方法
ニュートンの運動の第一法則
を改良して
ニュートンの運動の第一法則相対性理論補正
とする
###############
物体は、他の全ての物体から十分離れて
なんの影響も受けない状態では
静止または相対性理論による慣性抵抗を受ける
これを相対性理論補正の慣性の法則とする
###############
v≪cとして
直線運動の慣性抵抗は
Rs=-0.5(v/c)^2
円運動の慣性抵抗は
Rg=3(v/c)^2
合わせると
Rc=2.5(v/c)^2
Rx*86400[s/day]
Rx*2π[rad/周]
Rx*360*3600[秒/周]
とこうすれば
ニュートン力学も相対性理論位に
精密になると思います
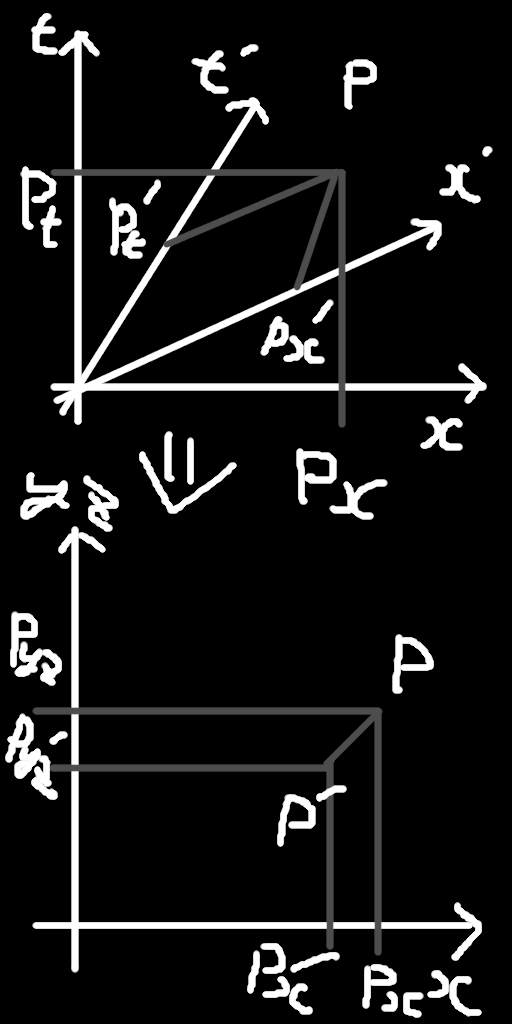
時空図とユークリッド系の変換をイメージすると
このようになり
上の時空図のローレンツ変換を
ユークリッド系にそのままローレンツ変換をプロットしたようになります
例えばvx=0.5cならば1/γ=√(1-(vx/c)^2)=0.866
x'=(1/γ)x=0.866xをプロットします
上の例は物体から見た系に変えるとするならばで
P系Aから見たP'系Bの運動距離はdab=vbta
なので
そもそも
ローレンツ変換をプロットする必要もなく
そのままdab=vbta
をプロットして
ユークリッド系全てがAから見た系として
あと気を付けるのは相対論的速度合成則だけなん
################
計算例
L=1光年v=0.5c
特殊相対性理論
a=√(1-(v/c)^2)=0.866
La/v=1.732[年]
相対性理論的慣性抵抗
a'=1-0.5(v/c)^2=0.875
La'/v=1.75[年]
L=1光年v=0.3c
特殊相対性理論
a=√(1-(v/c)^2)=0.954
La/v=3.18[年]
相対性理論的慣性抵抗
a'=1-0.5(v/c)^2=0.955
La'/v=3.18[年]
GPS衛星
1日86400[s]
速度4000[m]
理論値38.4e-6[s/日]
相対性理論的慣性抵抗
a'=(2.5(v/c)^2×86400)
=(4.45e-10×86400)
=38.5e-6[s/日]
水星摂動
水星の平均軌道速度V=47872.5[m/s]
理論値5.018744e-7[rad/周]
相対性理論的慣性抵抗
a'=(3(v/c)^2×2π)
=(7.6498349399367428992618e-8×2π)
=4.806533e-7[rad/周]
また秒/100年当たりにするには
2πの代わりに360*3600をかけ
100年で水星は415周するからそれをさらにかけると
(7.6498349399367428992618e-8×360×3600×415)=41.14[秒/100年]
と43[秒/100年]の観測結果が出せる
一般相対性理論による効果
太陽に近い軌道を持つほど一般相対性理論の効果は大きくなる
水星の近日点移動のニュートン理論からのずれは
一般相対性理論を検証するための初期の証拠になった
下の表に、水星から火星までの惑星の相対論的な近日点移動量を示す
| 惑星 | 理論(秒/100年) | 慣性抵抗(秒/100年) | 観測(秒/100年) |
| 水星 | 42.98 | 41.14 | 43.11 ± 0.45 |
| 金星 | 8.6 | 8.6 | 8.4 ± 4.8 |
| 地球 | 3.8 | 3.39 | 5.0 ± 1.2 |
| 火星 | 1.4 | 1.32 | 1.5 ± 0.15 |
慣性抵抗
水星軌道速度47872.5[m/s]公転周期88日1年4.15周
3×(47360/299792458)^2×360×3600×4.15×100=41.14
金星軌道速度35020[m/s]公転周期225日1年1.633周
3×(35020/299792458)^2×360×3600×1.633×100=8.6
地球軌道速度28000[m/s]公転周期365日1年1周
3×(28000/299792458)^2×360×3600×1.0×100=3.39
火星軌道速度24000[m/s]公転周期687日1年0.53周
3×(24000/299792458)^2×360×3600×0.53×100=1.32
近日点移動理論値
dφ=2π(3/2)(a/l)=2π(3/2)(a/((L/2)(1-e^2)))[rad/周]
dφ=360*3600(3/2)(a/((L/2)(1-e^2)))[秒/周]*[周/年]*[年]
1[AU]=149598700000[m]
太陽のシュバルツシルト半径a=2953[m]
水星軌道速度47872.5[m/s]
水星の離心率e=0.20563
水星の軌道長半径L/2=0.3871[AU]
水星4.15[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒/100年]
dφ=360*3600*3*(v/c)^2*4.15*100=360*3600*3*(47872.5/299792458)^2*4.15*100=41.14[秒/100年]
金星軌道速度35020[m/s]
金星の離心率e=0.0068
金星の軌道長半径L/2=0.7233[AU]
金星1.633[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.7233)/(1-0.0068^2)*1.633*100=8.6[秒/100年]
dφ=360*3600*3*(v/c)^2*1.66*100=360*3600*3*(35020/299792458)^2*1.66*100=8.6[秒/100年]
地球軌道速度28000[m/s]
地球の離心率e=0.0167
地球の軌道長半径L/2=1.0[AU]
地球1.0[周/年]
dφ=360*3600*3/2*2953/(149598700000*1.0)/(1-0.0167^2)*1.0*100=3.8[秒/100年]
dφ=360*3600*3*(v/c)^2*1.0*100=360*3600*3*(28000/299792458)^2*1.0*100=3.39[秒/100年]
火星軌道速度2400[m/s]
火星の離心率e=0.0934
火星の軌道長半径L/2=1.5237[AU]
火星0.53[周/年]
dφ=360*3600*3/2*2953/(149598700000*1.5237)/(1-0.0934^2)*0.53*100=1.34[秒/100年]
dφ=360*3600*3*(v/c)^2*0.53*100=360*3600*3*(24000/299792458)^2*0.53*100=1.32[秒/100年]
GPS衛星
1日86400[s]
速度4000[m]
一般理論値45.6e-6[s/日]
軌道半径26562000
軌道長166893968.1293
周期41723[s]
0.48291[日/周]
理論値22.02e-6[s/周]
22.02e-6/41723*2π=3.31e-9[rad/周]
慣性抵抗3(v/c)^2*2π=3.35e-9[rad/周]
特殊で大雑把に無理矢理
1/γ=√(1-(v/c)^2)=0.99999999991099
軌道長の縮み166893968.1293*0.99999999991099=166893968.1144
1周オーバーラン166893968.1293/166,893,968.1144=1.00000000008898
1.00000000008898×2π=5.59e-10[rad/周]
これは却下して
(0.99999999991099-1.0)×2π=-5.59266324192e-10[rad/周]
特殊慣性抵抗-0.5(v/c)^2
一般慣性抵抗3.0(v/c)^2
だから-6.0倍して3.3555979e-9[rad/周]
大雑把な計算だけれど水星摂動を無理矢理特殊相対論で計算すると
水星軌道速度47872.5[m/s]公転周期88日1年4.15周公転半径2439700軌道長15329087.193926
1/γ=√(1-(v/c)^2)=0.99999998725
(0.99999998725-1.0)×2π=-8.0110612666e-8[rad/周]
特殊慣性抵抗-0.5(v/c)^2
一般慣性抵抗3.0(v/c)^2
だから-6.0倍して4.80663676e-7[rad/周]
理論値は5.018744e-7[rad/周]でした
つまり円軌道の特殊相対論効果は
1/γ=√(1-(v/c)^2)
(1/γ-1.0)×2πで
一般相対論効果はその-6.0倍
合わせると-5.0倍
みたいな
だからまとめると
GPS衛星
速度4000[m/s]
高度26556752[m]
特殊相対論効果-7.2e-6[s/day]
一般相対論効果45.6e-6[s/day]
足して38.4e-6[s/day]
と理論値があって
軌道長166893968.1293
周期41723[s]
0.48291[日/周]
特殊理論値-7.2e-6*0.48291=3.4769e-6[s/周]
3.4769e-6/41723*2π=-5.23604e-10[rad/周]
一般理論値45.6e-6*0.48291=22.02e-6[s/周]
22.02e-6/41723*2π=3.31e-9[rad/周]
合わせた理論値38.4e-6*0.48291=18.5437e-6[s/周]
18.5437e-6/41723*2π=2.792555e-9[rad/周]
となって
1/γ=√(1-(v/c)^2)=0.9999999999109879955
特殊理論値
(1/γ-1.0)×2π=-5.5927891e-10[rad/周]
一般理論値3.35567351e-9[rad/周]
合わせた理論値2.7963945938e-9[rad/周]
なわけ
(1/γ-1.0)が特殊相対論効果でそれに2πかけると[rad/周]になるん
[s/day]にするには
[rad/周]/2π*周期[s]*[周/day]なわけ
例えば
金星理論8.6[秒/100年]軌道速度35020[m/s]公転周期225日1年1.633周
相対論慣性抵抗
3×(35020/299792458)^2×360×3600×1.633×100=8.6
特殊から計算
1/γ=√(1-(v/c)^2)=0.9999999931772276
(1/γ-1.0)×-6.0×360×3600×1.633×100=8.6
こんな感じ
つまり特殊相対論を円軌道にしたら一般相対論効果は
特殊相対論効果に-6.0倍かければいいよってこと
水星軌道速度47872.5[m/s]
水星の離心率e=0.20563
水星の軌道長半径L/2=0.3871[AU]
水星4.15[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒/100年]
dφ=360*3600*3*(v/c)^2*4.15*100=360*3600*3*(47872.5/299792458)^2*4.15*100=41.14[秒/100年]
水星の100年経過した摂動座標を求めると
42.9[秒/100年]/360/3600*2π=2.07985e-4[rad/100年]
水星の短半径=0.3075[AU]
水星の長半径=0.4667[AU]
(x,y)=(0.3075cosθ,0.4667sinθ)=(3.074999e-1,1.6941e-6)
となります
つまりユークリッド座標系でもこれが出ていればいいってこと
################
速度合成則
ある座標系K
Kに対して速度Vの等速運動を
している座標系K'
x軸ブーストに回転して
その速度合成則は
γ=(1-0.5(V/c)^2)とし
v'x=(vx-V)/(1-(vxV/c^2))
v'y=(vy/(1-(vxV/c^2)))γ
v'z=(vz/(1-(vxV/c^2)))γ
vx=(v'x+V)/(1+(v'xV/c^2))
vy=(v'y/(1+(v'xV/c^2)))γ
vz=(v'z/(1+(v'xV/c^2)))γ
x軸ブーストしたら元の回転に戻す
ソースコード参照
[./javascripts/nas6lib/rngkt.js(N6LRngKt.VelocityAdd3D())]
################
計算例
速度w(0.5c,0.25c,0.25c)に
速度W(-0.25c,-0.25c,-0.5c)を加える
x軸ブーストに回転する
w・x=(-0.25)c^2=-0.25c^2
左右手系の符号s=w・xの符号×-1
|w|=√(0.25+0.125+0.125)c=0.707c
|x|=c
cosΘ=(w・x)/|x||w|=-0.353607
wとxのなす角Θ=s×(cos^-1Θ)=1.93222
垂直ベクトルを回転軸とする
A=w×x=(0,0.25,-0.25)
wをA軸周りに回転
q=cos(Θ/2)+Asin(Θ/2)
=(0.568504,0,-0.2056701,0.2056701)
○○○|1-2y^2-2z^2○2xy-2wz○2zx+2wy|
Rq=○|2xy+2wz○1-2x^2-2z^2○2yz-2wx|
○○○|2zx-2wy○2yz+2wx○1-2x^2-2y^2|
○○○|1.1692○0.233849○0.233849|
Rq=○|-0.233849○0.915399○-0.0846|
○○○|-0.233849○-0.0846○0.915399|
行列をノーマライズする
|Rq[0]|=2.052894
|Rq[1]|=0.899798
|Rq[2]|=0.899798
○○○|0.569537○0.113912○0.113912|
Rqn=○|-0.25989○○○1○○○-0.094021|
○○○|-0.25989○-0.094021○○○○○1|
RqnW=(-0.44934c,-0.138017c,-0.411522c)=v'
V=(0.707c,0,0)
γ=(1-0.5(V/c)^2)=0.7500755
vax=(v'x+V)/(1+(v'xV/c^2))
=(-0.44934c+0.707c)/(0.682317)
=(0.25766c)/(0.682317)=0.377625c
vay=(v'y/(1+(v'xV/c^2)))γ
=(-0.138017c/(0.682317))0.7500755
=-0.151723c
vaz=(v'z/(1+(v'xV/c^2)))γ
=-0.452389c
v=va=(0.377625c,-0.151723c,-0.452389c)
元の回転に戻す
q'=cos(-Θ/2)+Asin(-Θ/2)
=(0.568504,0,0.2056701,-0.2056701)
○○○|0.569537○-0.113912○-0.113912|
R'qn=○|0.25989○○○1○○○-0.094021|
○○○|0.25989○-0.094021○○○○○1|
R'qnv=(0.283887c,-0.011048c,-0.339983c)=w'
ガリレイ変換における
w+W=(0.25c,0,-0.25c)
と求められた
w'=(0.283887c,-0.011048c,-0.339983c)
比べて、まあ妥当なんじゃないかと思います
ガリレイ変換に比べて加速しているのは
時間の縮みのせいなんじゃないかなあ
よってwにWを加えてw'が求められた
もっと単純な計算例
速度w(0.5c,0,0)に
速度W(0.25c,0,0)を加える
vax=(v'x+V)/(1+(v'xV/c^2))
=(0.5c+0.25c)/(1.125)
=0.667c
vay=(v'y/(1+(v'xV/c^2)))γ
=0
vaz=(v'z/(1+(v'xV/c^2)))γ
=0
v=va=(0.667c,0,0)
################
速度加速則
速度v,加速度a,時間dtのとき
|v|において最大値の軸をnとすると
v(n以外二つ)=√((1-v(n)^2)/2)
vab=tanh(|a|dt)
vac=(|v|+vab)/(|v|vab+1)
ret=(v+adt)
もしも1<vacだったら
ret=ret/vac
ソースコード参照
[./javascripts/nas6lib/rngkt.js(N6LRngKt.VelocityAccl3D())]
################
後はルンゲクッタ法で積分をすれば完成
ソースコード参照
[./javascripts/nas6lib/rngkt.js(N6LRngKt.accel())]
[./javascripts/nas6lib/rngkt.js(N6LRngKt.UpdateFrame())]
################
宇宙空間は静止している?
ニュートンの運動の第一法則相対性理論補正
とする
###############
物体は、他の全ての物体から十分離れて
なんの影響も受けない状態では
静止または相対性理論による慣性抵抗を受ける
これを相対性理論補正の慣性の法則とする
###############
つまりこの定義だとすると物体は完全絶対停止を保持することになりますが
私がこれが間違っていないと思うのは
地球や太陽近傍の宇宙空間で太陽系がある方向に動いているとするならば
相対性理論の速度合成則により動いている方向に物体が加速しづらい
という加速等方性の破れがあるはずですが
現実的には加速等方性があると聞きます
加速等方性があるということはその空間は絶対静止系であるということです
相対性理論が絶対静止系を否定したのですが
その相対性理論の速度合成則により
加速等方性があるから宇宙空間は絶対静止系であるということになってしまいます
なんとも皮肉な話ですね
でもそのほうが3Dエンジンの実装そのまんまなので都合がいいですね
絶対静止系がグローバル座標であり
慣性抵抗が結局その絶対静止系を形成する
そういうのがプログラミングに実に都合がいいです
コンピューターワールドですよん
また対称性の破れは
そもそも恒星と惑星、惑星と衛星という
親子関係であるから完全対称性は初めからないんです
それと単純な球であれば果てがありますが
トーラス面(ドーナツ、リンゴ)は
果てがない(真っ直ぐに進んで振出しに戻る)ので
宇宙空間はトーラス面になっているんでしょうね
ま、数学的にはクォータニオンの四元球なんだけどね
軸の直交には虚数を用いるのが便利であり
(gds)^2=(chdt)^2+(idx)^2+(jdy)^2+(kdz)^2
c:光速度、ghijk:軸虚部、dtdxdydz:軸、ds:世界距離
こんな感じのクォータニオンになってるんだと思います
2次元は
(kr)^2=(ix)^2+(jy)^2
r:半径、xy:実部、ijk:虚部
何でこんな風にするかというと
回転行列は
|cosθ〇-sinθ|=R(θ)
|sinθ〇cosθ|
回転行列の積は
|cosφ〇-sinφ||cosθ〇-sinθ|=R(φ)R(θ)
|sinφ〇cosφ||sinθ〇cosθ|
計算すると
|cosφcosθ-sinφsinθ〇-cosφsinθ-sinφcosθ|
|sinφcosθ+cosφsinθ〇-sinφsinθ+cosφcosθ|
加法定理より
|cos(θ+φ)〇-sin(θ+φ)|=R(φ)R(θ)
|sin(θ+φ)〇cos(θ+φ)|
だからφ=θならば
|cos(2θ)〇-sin(2θ)|=R^2(θ)=R(2θ)
|sin(2θ)〇cos(2θ)|
2回θ回転するんだから2θもそりゃそうですね
ここでθ=π/2の時
|-1〇0|=R^2(π/2)=R(π)=-I
|0〇-1|
つまりθ=π/2回転において回転の2乗は-1倍の単位行列Iです
このことから虚軸とは実軸からπ/2回転しているということです
こういうことを考えると
(kr)^2=(ix)^2+(jy)^2
r:半径、xy:実部、ijk:虚部
と2次元はこんな感じになるんです
まぁ、こんな長ったらしい説明じゃなくても
π/2を2回回転する時、結局πの回転だから負の単位行列になり
つまり直交軸とは虚軸(X^2=-I)である
なんだけれどね
また、時間と座標について考えると
時間の単位行列に対して時間の負の単位行列は?
ということだから、もちろん
速度に対して負の速度になるから
v^2=(dr/dt)^2=(dx^2+dy^2+dz^2)/(dt)^2
でこれにおいて
(gds)^2=(chdt)^2+(idx)^2+(jdy)^2+(kdz)^2
c:光速度、ghijk:軸虚部、dtdxdydz:軸、ds:世界距離
軸虚部は
-h^2/α=i^2+j^2+k^2,α:係数
こんな関係性があるということです
負の時間は負の速度の座標変化だから
空間3軸をまとめたものと時間軸は直交する虚軸の関係にあると言えるん
(ds)^2=(cidt)^2+(dx)^2+(dy)^2+(dz)^2
これはまんま相対論ですね
軸の直交とは
内積dot=|x||y|cosθ
であり
例えばxのy軸回転において
π/2回転はdot=0
π/2回転の2回回転のπ回転はdot=-1
になるよんってことなんす
で、そんなわけでクォータニオンは
q=w+xi+yj+zk
ですが
つまりxyz軸はそれぞれ直交して
wつまり時間軸tと空間座標xyzの間の関係も直交する
v=(dr/dt)=√(dx^2+dy^2+dz^2)/dt
-v=-(dr/dt)=-√(dx^2+dy^2+dz^2)/dt
の関係性ということで世界記述なんです
ああ、だからむしろ
クォータニオンのwつまり速度軸vと空間座標xyzの間の関係も直交する
なんね
ですので、世界を一番簡単に数式化すると
v=(dr/dt)=√(dx^2+dy^2+dz^2)/dt
world=v+xi+yj+zk
こんな感じやろ
速度vの空間座標に対するπ回転つまり-vだから
v=(dr/dt)=√(dx^2+dy^2+dz^2)/dt
-v=-(dr/dt)=-√(dx^2+dy^2+dz^2)/dt
こうなっていて速度軸vと空間座標xyzが直交軸関係にあるんです
world=v+xi+yj+zk
は
world=vh+(r/t)h:r:二点間距離t:二点間時間h:速度虚軸
とも書けるん
だから世界つまり動きあるいは全ては、速度だ
って話
止まっているんだけど止まらないん
静止した世界では、動きが全てだ
あれ?ちょっと待てよ整理する
クォータニオンは
q=w+xi+yj+zk
であって
wとxyzの関係性は
1s間に光の進んだ距離から物体の進んだ距離の差ってなってん
だから相対性理論では、計量を(ci,1,1,1)ととって
(ds)^2=(cidt)^2+(dx)^2+(dy)^2+(dz)^2
だけれど
これをクォータニオン的に記述すれば、計量を(c,i,j,k)ととれば
(ds)^2=(cdt)^2+(idx)^2+(jdy)^2+(kdz)^2
ってこういう風に言いたかったん
空間のxyz軸は互いに直交だから時間軸を虚軸に取るより空間を虚軸に取った方がより厳密なん
また
1s間に物体の進んだ距離と
-1s間に物体の進んだ距離の間には
負の単位行列がかかるから空間xyzと時間tは虚軸の関係なん
だから1s間に光の進んだ距離^2から物体の進んだ距離^2の差ってなってん
虚軸であるっていうのは片方の軸周りにπ/2を2回回転したπ回転が負の単位行列であるということね
まとめて
相対論の世界距離をクォータニオン的に記述すれば、計量を(c,i,j,k)ととって
(ds)^2=(cdt)^2+(idx)^2+(jdy)^2+(kdz)^2
虚軸の関係であるっていうのは片方の軸周りにπ/2を2回回転したπ回転が負の単位行列であるということ(R^2(π/2)=-I)
そのうえで、
特殊相対論補正(直線運動)は
-0.5(v/c)^2
一般相対論補正(円運動)は
3.0(v/c)^2
合わせて
2.5(v/c)^2
となっているので
F=-(GMm/r^2)(1+2.5(v/c)^2)
F=-(GMm/r^2)(1+αv^2)
という形になっているならば
αvっていうのはいわゆる慣性抵抗であるから
ニュートンの運動の第一法則相対性理論補正
###############
物体は、他の全ての物体から十分離れて
なんの影響も受けない状態では
静止または相対性理論による慣性抵抗を受ける
これを相対性理論補正の慣性の法則とする
###############
になるん
で、これに速度合成則と加速度合成則を考えて
積分をルンゲクッタ法ですれば
おおよそ相対論くらいの精密さの
物理エンジンの出来上がりなわけ
別におらが何をしたかって言うと相対論の計算を
画面表示するにあたって
リーマン幾何からユークリッド幾何に変換しただけのことでやんす
GPS衛星
1日86400[s]
速度4000[m]
1日軌道長L=345600000[m]
理論値38.4e-6[s/日]
a=(1+38.4e-6)=1.0000384
La/v=86403.31776
(86403.31776/86400-1)=38.4e-6[s/日]
相対性理論的慣性抵抗
a'=(1+2.5(v/c)^2×86400)
=(1+4.45e-10×86400)
=(1+38.5e-6)=1.0000385
La'/v=86403.3264
(86403.3264/86400-1)=38.5e-6[s/日]
こういう風にちゃんとほぼ理論値と同じ値が出るんだから
あとは
ユークリッド幾何で相対論を取り扱うにあたって
相対論的速度合成則と相対論的加速度合成則を考慮して
積分をルンゲクッタ法ですりゃあいいのよん
とある資料によれば太陽系はとある方向にCMBと比較して秒速600000[m/s](0.002c)で公転しているそうな
それでは速度合成則で確かめてみよう
まずは公転方向にさらに公転速度だけ速度合成する場合
0.002c=599584[m/s]
速度w(0.002c,0,0)に
速度W(0.002c,0,0)を加える
vax=(v'x+V)/(1+(v'xV/c^2))
=(0.002c+0.002c)(1+(0.002c*0.002v/c^2))
=0.003999984c
vax-wx=0.001999984c
=599580[m/s]
だけ公転方向に加速した
次に鉛直方向にさらに公転速度だけ速度合成する場合
速度w(0.002c,0,0)に
速度W(0,0.002c,0)を加える
vax=(v'x+V)/(1+(v'xV/c^2))
=(0+0.002c)/(1)
=0.002c
γ=(1-0.5(V/c)^2)
=(1-0.5(0.002c/c)^2)
=0.999998
vay=(v'y/(1+(v'xV/c^2)))γ
=(0.002c/(1)0.999998
=0.001999996c
vaz=(v'z/(1+(v'xV/c^2)))γ
=0
v=va=(0.002c,0.001999996c,0)
z=v-w=(0,0.001999996c,0)
zy=0.001999996c
=599583[m/s]
だけ鉛直方向に加速した
つまり太陽系が0.002c(599584[m/s])でとある方向に公転しているのならば
0.002cの速度合成に対して
公転方向では0.001999984c(599580[m/s])の速度合成を示し
鉛直方向では0.001999996c(599583[m/s])の速度合成を示すはずである
ゆえに太陽系の公転方向に加速しづらいという 加速度等方性(速度合成等方性)の破れがあるはずです
さて 果たして 一体いつ この加速度等方性の破れは 観測されたのでしょうか?
おらの考えでは銀河系は回転しているのではなく
爆発して(?)そのうち停止した ではないかなぁ?
銀河系くらいのスケールでは 恒星を公転させるほど万有引力は 働かないんじゃないかなぁ?
一般に
太陽 28000光年 よりも内側の質量 1.0e11 Msun
中心核円盤 2000光年 よりも内側の質量 5.7e9 Msun
中心核付近のリング 5光年 よりも内側の質量 3.5e6 Msun
だそうで
太陽 28000光年 よりも内側の質量 1.0e11 Msun
1.0e11 Msunの大部分がダークエネルギーダークマターによるものらしいですが
で 物質の質量はそのうちの4%だそうで
いっそのことダークエネルギーダークマターなどはないとして4%として
太陽 28000光年 よりも内側の物質質量 4.0e9 Msun
として計算すると
v=√(Gm/r)=44882[m/s]
だから太陽の公転速度は地球の公転速度の1.5倍程度まで減速していて
その程度の速度だから加速度等方性の破れが観測されないのでは?
銀河系を 無理矢理 回転体と考えるから 存在しない ダークエネルギー ダークマター が必要なのでしょう?
ダークエネルギー ダークマター の存在を 疑うと 銀河系は 回転体というよりは 渦巻花火のようなものを イメージしてしまう
存在しない(観測されたことのない) ダークエネルギー ダークマター による理論が なぜ正しいのでしょうか?

こんな感じの渦巻花火の銀河系なんじゃね?
銀河系が別に重力で縛ってなくて ただまき散らしてるだけならば ダークエネルギー も ダークマター も 要らないんです
単なる打ちっぱなしゴルフ場です
科学は 実在の証拠がなければ ないと考えるのでは なかったのですか?
- 天の川銀河 ダークマターの考慮なしのシミュレート -
ファイルはこちら
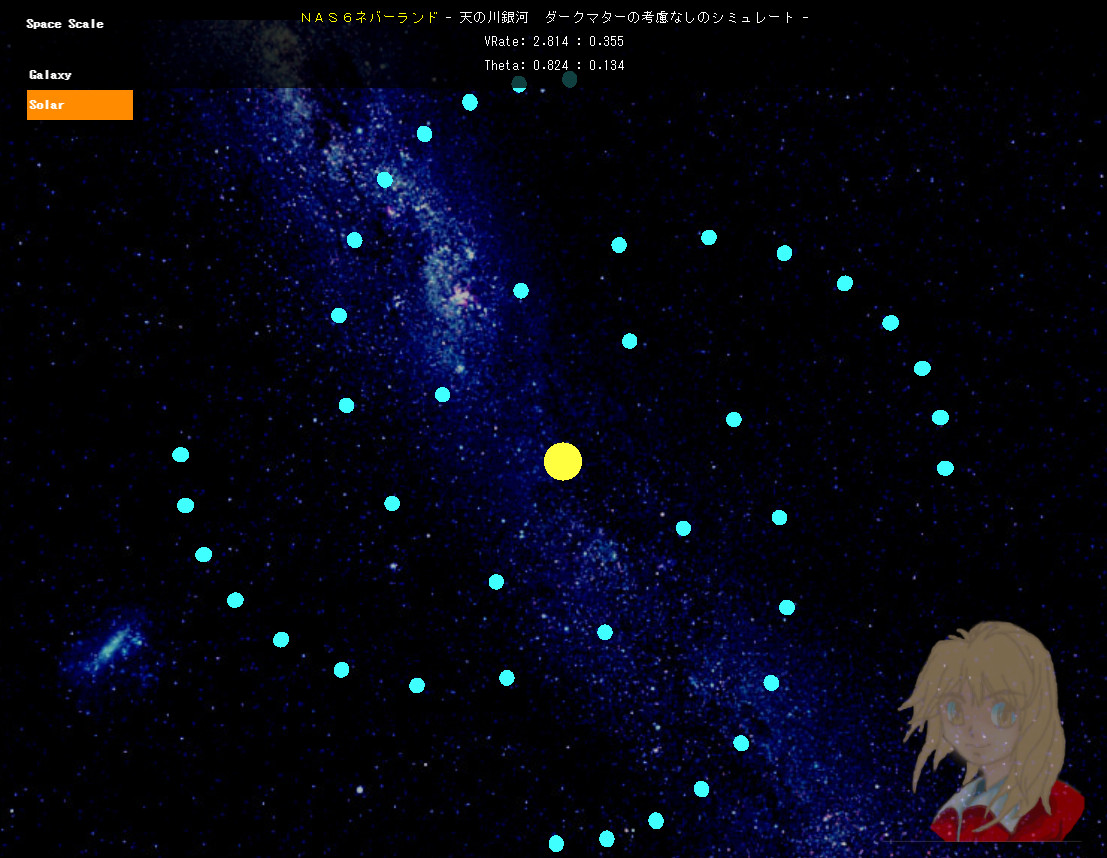
銀河の腕の要素はかなりつぶれた楕円軌道というシミュレートならば
ダークマターが無くても腕の要素の軌道速度が大体一定でも構いません
こんな感じで銀河系が動いているんじゃないですか?
ダークマターなんてないんです
万有引力が銀河スケールでおかしいというのは補正項が足りないのだなと思い
F:力:G:万有引力定数:M:質量:m:質量:r:距離:S:相対性理論補正項:GR:NAS6補正項
F=-(GMm/r^2)(1+S+GR)
この形に持っていくことを考える
銀河スケールでの観測結果の表
| R |
M/Msun |
V |
RV^2/GM/Msun |
| 2.65e20 |
1.0e11 |
2.2e5 |
1.78e30 |
| 1.9e19 |
5.7e9 |
2.0e5 |
2.0e30 |
| 4.7e16 |
3.5e6 |
1.0e5 |
1.98e30 |
| 1.0e12 |
18.7 |
0.5e5 |
2.004e30 |
RV^2/GM/MsunつまりMSun^2
(GMm/R)(1+S+GR)=W=mAR=mV^2
であるから
(RV^2/GM)=1+S+GR
右辺の1+Sは影響ないとして無視して上記の表と比べると
(RV^2/GM)=(MSun^2)一定で(MSun^2)の逆数をとれば
(RV^2/GM)=(MSun^2)一定に収束するだろうと思うので
GR=1/(MSun^2)=1/4e60
ではないかと推察される
GR(GMm/R)=mAR=mV^2
GR=RV^2/GM???あれ?おかしいな?多分逆数だ
これをNAS6補正項(万有斥力補正項)とし最終的に完全な万有引力の式は
完全な万有引力方程式
F=-(GMm/R^2)(1+S+GR)=
-(GMm/R^2)(1+2.5(v/c)^2-1/Msun^2)=
-(GMm/R^2)(1+2.5(v/c)^2-1/4.0e60)
となりました
ダークマターなんてないんです
銀河系は重力を振り切っていて単なる打ちっぱなしゴルフ場です
ちなみにNAS6補正項GRの次元は
GM/RV^2=([m^3/kgs^2][kg])/([m][m^2/s^2])=[1/1]
無次元です
このような万有引力を用いてシミュレーションして銀河スケールでは
恒星が中心重力を振り切って観測通りに回転半径によらずほぼ速度を保ち続けるような
計算が出来ました
NAS6補正項の符号を負にしたのは銀河系くらいの大きさでは半径によらず
速度が一定ということなので引力補正ではなく斥力補正としました
この補正項はごく僅かなので重力が大きいところでは何も作用しませんが
重力圏から離れたところで極微弱な斥力として働きます
これを万有斥力とかダークエネルギーとか呼びたきゃ呼べばいいけれど
おらは銀河系で恒星の速度が半径によって減衰しないってところで
万有引力を補正しただけです
(GMm/R^2)/(MSun^2)の項を追加して万有斥力としたん
なぜならば様々な状態で(RV^2/GM)が(MSun^2)で一定のようだからです
もちろん従来の万有引力を邪魔しないし銀河系スケールの振る舞いも説明できるからちょうどいいやってことで
積分係数の1/2をどうしようかと考えたけれどMSun^2がシンプルでいいかなと思って
1/2は掛けないことにしました
この世界の宇宙を語るうえで
R:半径:V:軌道速度:G:万有引力定数:M:質量:Msun:太陽質量
(RV^2/GM)=(MSun^2)一定
は大切な関係だと思います
↑の式を変形してかもしれないけれど
r:半径:rs:重力源シュワルツシルト半径:v:軌道速度:c:光速度
rs/r=2(v/c)^2
この関係も大事かな
自然界の安定した天体の軌道は多分殆どこの関係を持っています
2r(V/c)^2=rs
太陽のシュワルツシルト半径rs=2953[m]
光速度c=299792458[m/s]
| 惑星名 |
軌道長半径r[m] |
平均軌道速度V[m/s] |
rs=2r(V/c)^2 |
| 水星 |
57909656770 |
47872.5 |
2953.328771 |
| 金星 |
108208930000 |
35021.4 |
2953.37571 |
| 地球 |
149597870700 |
29780 |
2952.31972872 |
| 火星 |
227936640000 |
24130.9 |
2953.5870263 |
| 木星 |
778412010000 |
13069.7 |
2958.893649 |
| 土星 |
1426725400000 |
9672.4 |
2970.2806 |
| 天王星 |
2870990000000 |
6800 |
2954.18776416 |
| 海王星 |
4495060000000 |
5500 |
3025.8644 |
RV^2/GM/Msun=MSun^2一定
銀河スケールでの観測結果の表
| R |
M/Msun |
V |
RV^2/GM/Msun |
| 2.65e20 |
1.0e11 |
2.2e5 |
1.78e30 |
| 1.9e19 |
5.7e9 |
2.0e5 |
2.0e30 |
| 4.7e16 |
3.5e6 |
1.0e5 |
1.98e30 |
| 1.0e12 |
18.7 |
0.5e5 |
2.004e30 |
■■■ 量子力学も考慮してみる ■■■
u''+u=m/h^2+3mu^2
において
u''+u=m/h^2
は万有引力
F=-(GmM/r^2)
に相当する
ここで
波動方程式
Ψ=expiθ=軌道速度Vかなあ?
h=r^2dψ/ds,m=kM/c^2,u=1/r,u''=1/6r^3
をu''+u=m/h^2に代入して
1/6r^3+1/r=(kM/c^2)/(r^2dψ/ds)^2
(1+6r^2)/6r^3=(kM/c^2)/(r^4(dψ/ds)^2)
(1+6r^2)(r^4(dψ/ds)^2)/6r^3(kM/c^2)=1
(r^4(dψ/ds)^2+6r^6(dψ/ds)^2)/(6r^3kM/c^2)=1
c^2((r/6)(dψ/ds)^2+r^3(dψ/ds)^2)/kM=1
((r/6+r^3)(dψ/ds)^2)/m=1
((r/6+r^3)(dt/dt)^2(dψ/dt)^2(dt/ds)^2)/m=1
dt/ds=1/c
((r/6+r^3)(dψ/dt)^2(1/c^2))/m=1
((r(1/6+r^2))(dψ/dt)^2(1/c^2))/m=1
rdψ/dt=軌道速度V
(((V/c)^2/r)(1/6+r^2))/m-1=0
は
F=-(GmM/r^2)
と同じ
縦軸を虚軸ととった軌跡
■■■ 3Dプログラミング入門講座 ■■■
NAS6LIB
ポリゴンテスト解説・x3dom使い方
その1:ベクトル
その2:行列
その3:クォータニオン
その4:基本総復習・実践
その5:応用その1・メッシュアニメーション、動的テクスチャ
その6:応用その2・GLSL、カスタムシェーダー、キーボード、ファイル
その7:応用その3・ゲームプログラミング、タグの動的追加
その8:応用その4・GLSL、シェーダー、その2
その9:物理演算その1・電卓で相対性理論を解く方法
その10:物理演算その2・相対性理論的ニュートン力学
その11:物理演算その3・ケプラー方程式で惑星軌道シミュレーターを作る
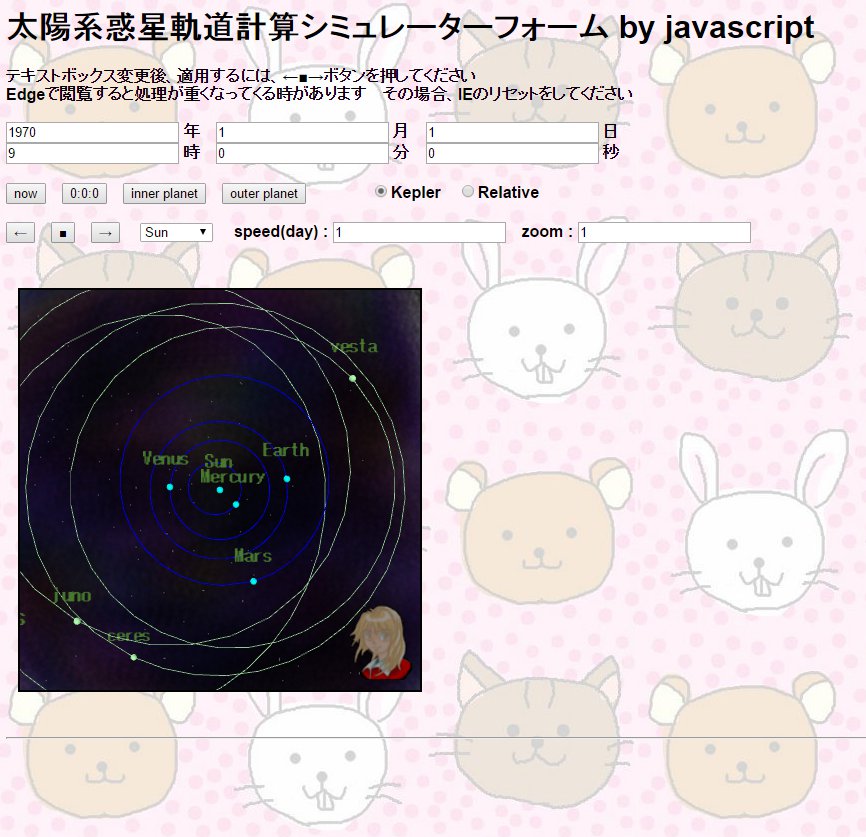
その12:物理演算その4・ルンゲクッタ法で作った
相対性理論的ニュートン力学物理エンジンで惑星軌道シミュレーターを作る
その13:経路探索(A*:A-STAR)&巡回セールスマン問題 : 巨大サイズ : くろにゃんこ
その14:プログラミングにおける配列テーブルテクニック
その15:javascriptのクラス活用法
その16:透視射影公式テスト
その17:ケプラー方程式カプセルライブラリ使用法
その18:CSVファイル処理
その19:物理演算その5・重力多体問題
その20:同次座標について(3D座標系の基本の基本)
その21:おさらいコモンクラスの宣言
その22:物理エンジンライブラリ解説(ケプラー方程式・ルンゲクッタ・相対論的万有引力)
■■■ THREE.JSプログラミング講座 ■■■
THREE.JSテスト解説・THREE.JS使い方
THREE.JS examplesをいじってみた(フレネル反射透過シェーダー)

THREE.JS (半透明シェーダー)
THREE.JS 3D演算で必要な計算(具体例)★とても重要★
THREE.JS THREE-VRM をいじってみた

<<prev 電卓で相対性理論を解く方法 : ケプラー方程式で惑星軌道シミュレーターを作る next>>
戻る










