3Dプログラミング入門講座・その9:物理演算その1・電卓で相対性理論を解く方法
相対性理論的ニュートン力学
電卓で相対性理論を解く方法
特殊相対性理論は
F=-(GmM/R^2)(1-0.5(V/C)^2)
一般相対性理論は
F=-(GmM/R^2)(1+3.0(V/C)^2)
特殊と一般合わせて
F=-(GmM/R^2)(1+2.5(V/C)^2)
これを電卓でポチポチやれば解けます
また離心率eからこれをまとめると
F=-(GmM/R^2)(1+(3.0-3.5(1-e))(V/C)^2)
あるいは
F=-(GmM/R^2)(1+(3.0-3.5(1-e)^2)(V/C)^2)
になるのではないかな?(*A)の考察は後述
後述の考察により
楕円軌道(離心率e)の一般相対性理論を考慮した万有引力運動方程式は
F=-(GmM/R^2)(1+(3.0/(1-e^2))(V/C)^2)
と解けました
F力G万有引力定数mM質点質量R質点間距離e離心率V軌道速度C光速度
またこれは変形したこの公式と等価です
楕円軌道(離心率e)の一般相対性理論を考慮した万有引力運動方程式は
F=-(GmM/R^2)(1+(3.0/(1-e^2))(a/L))
と解けました
F力G万有引力定数mM質点質量R質点間距離e離心率a太陽のシュバルツシルト半径L衛星の軌道長直径
一連の流れをまとめた証明はこちら
特殊の証明#################################################
ローレンツ収縮
a=√(1-(v/c)^2)
の近似は
a=1-0.5(v/c)^2
です
FA(v)=√(1-(v/c)^2)
FB(v)=1-0.5(v/c)^2
FA(1.0c)=0
FB(1.0c)=0.5
FA(0.99c)=0.14
FB(0.99c)=0.49
FA(0.8c)=0.6
FB(0.8c)=0.68
FA(0.5c)=0.866
FB(0.5c)=0.875
FA(0.2c)=0.979
FB(0.2c)=0.98
FA(0.1c)=0.994
FB(0.1c)=0.995
一般の証明#################################################
計量(c,i,j,k)のシュワルツシルト(球対称性を持つアインシュタイン方程式の真空解)の線素は
c光速度t座標時r動径座標θ余緯度座標φ経度座標2m=rsシュワルツシルト半径=2GM/c^2M質量
ds^2=(1-rs/r)c^2dt^2-dr^2/(1-rs/r)-r^2dθ^2-r^2sin^2θdψ^2
ds^2=(1-2m/r)c^2dt^2-dr^2/(1-2m/r)-r^2dθ^2-r^2sin^2θdψ^2・・・(*1)
その変分問題
δ∫((1-2m/r)c^2(dt/ds)^2-(dr/ds)^2/(1-2m/r)-r^2(dθ/ds)^2-r^2sin^2θ(dψ/ds)^2)ds=0・・・(*2)
各成分に対する方程式を導出すると
i=1,r,(*1)/ds^2
1=(1-2m/r)c^2(dt/ds)^2-(dr/ds)^2/(1-2m/r)-r^2(dθ/ds)^2-r^2sin^2θ(dψ/ds)^2・・・(*1A)
i=2,θ,
(d/ds)(r^2(dθ/ds))=r^2sinθcosθ(dψ/ds)^2・・・(*1B)
i=3,ψ,
(d/ds)(r^2sin^2θ(dψ/ds))=0・・・(*1C)
i=0,ct
(d/ds)((1-2m/r)(dt/ds))=0・・・(*1D)
成分を選んで
θはπ/2、dθ/ds=0、の赤道面上での話とし、θは定数なので(*1B)は無視する
ψは(*1C)よりr^2(dψ/ds)=h(定数)角運動量保存・・・(*3)
tは(*1D)より(1-2m/r)(dt/ds)=l(定数)エネルギー量保存・・・(*4)
(*1A)より
(1-2m/r)=(cl)^2-(dr/ds)^2-(h/r)^2(1-2m/r)・・・(*5)
rをψの関数として微分したものは
(d/dψ)(r(ψ))=r'=(dr/ds)(ds/dψ),(*3)より
(dr/ds)=r'(dψ/ds)=hr'/r^2,r=1/u,r'=-u'/u^2,(*5)より
(1-2mu)=(cl)^2-(hu')^2-(hu)^2(1-2mu)
u'^2=((cl)^2-1)/h^2+2mu/h^2-u^2+2mu^3・・・(*6)
ψで微分して
2u'u''=2mu'/h^2-2uu'+6mu^2u'・・・(*7)
u'=0,u=1/r(定数)という解は円軌道
u''+u=m/h^2+3mu^2・・・(*8)
この式はu''+u=m/h^2が万有引力の式に対応しイメージしてみると
シュワルツシルト時空の重力による加速度RelativeGravityの式は
r半径,G万有引力定数,M質量,V軌道速度,c光速度,S相対論補正項
Rg=-(GM/r^2)(1+S)
の形であるから、ここでh=r^2dψ/ds,m=kM/c^2,u=1/r,であって
相対論補正項3mu^2を検証すると、m/h^2でくくり
u''+u=(m/h^2)(1+3mu^2/(m/h^2)=(m/h^2)(1+S)の形にして、Sを調べます
3mu^2/(m/h^2)=3u^2h^2=3(1/r^2)(r^2dψ/ds)^2=3r^2((dt/ds)(dψ/dt))^2=3r^2(dψ/dt)^2(1/c^2)
=3(rdψ/dt)^2(1/c^2)
(rdψ/dt)は円の接線方向の速度だからそれを軌道速度Vとみれば3(V/c)^2と解けて
相対論補正項S=3(V/c)^2だから
ユークリッド幾何で
シュワルツシルト時空の重力による加速度RelativeGravityの式は
r半径,G万有引力定数,M質量,V軌道速度,c光速度,S相対論補正項
Rg=-(GM/r^2)(1+S)=-(GM/r^2)(1+3(V/c)^2)
と解ける
#####################################################
計算例
地球質量5.972e+24kg
地球半径6.371e+6[m]
光速度299792458[m/s]
一日86400[s]
GPS衛星
速度4000[m/s]
高度26556752[m]
特殊相対論効果-7.2e-6[s/day]
一般相対論効果45.6e-6[s/day]
足して38.4e-6[s/day]
相対論補正項は
特殊
-0.5(V/C)^2=-8.9e-11
一日当たり
-8.9e-11*86400=-7.69e-6
一般
3.0(V/C)^2=5.34e-10
一日当たり
5.34e-10*86400=4.61e-5
特殊+一般
2.5(V/C)^2=4.45e-10
一日当たり
4.45e-10*86400=3.85e-5
と微分方程式を解かずとも
電卓を何回か弾くだけで簡単に解けます
検証
F=-(GmM/r^2)(1+αV)の形に
なっているので
相対性理論補正とは
いわゆる慣性抵抗となっていて
通常の相対性理論では
同時の相対性(物体毎に時間軸がある)により
時刻合わせが大変で
世界を一つの画面で
表現する事は難しいのですが
これはユークリッド幾何と
なっているため
絶対時間の表現なので
世界を一つの画面で
表現出来ます
注釈:
上の計算では
時空の3+1分解というかもっと簡単に
極座標のr=√(x^2+y^2+z^2)
についての一日当たりの円周上の相対論補正項
を求めています
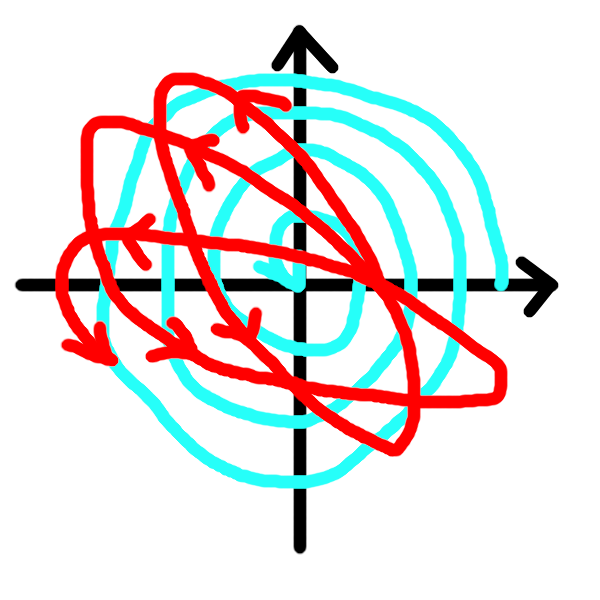
F=-(GmM/r^2)(1+S)のグラフ概要
赤色と水色の合成みたいな軌跡です
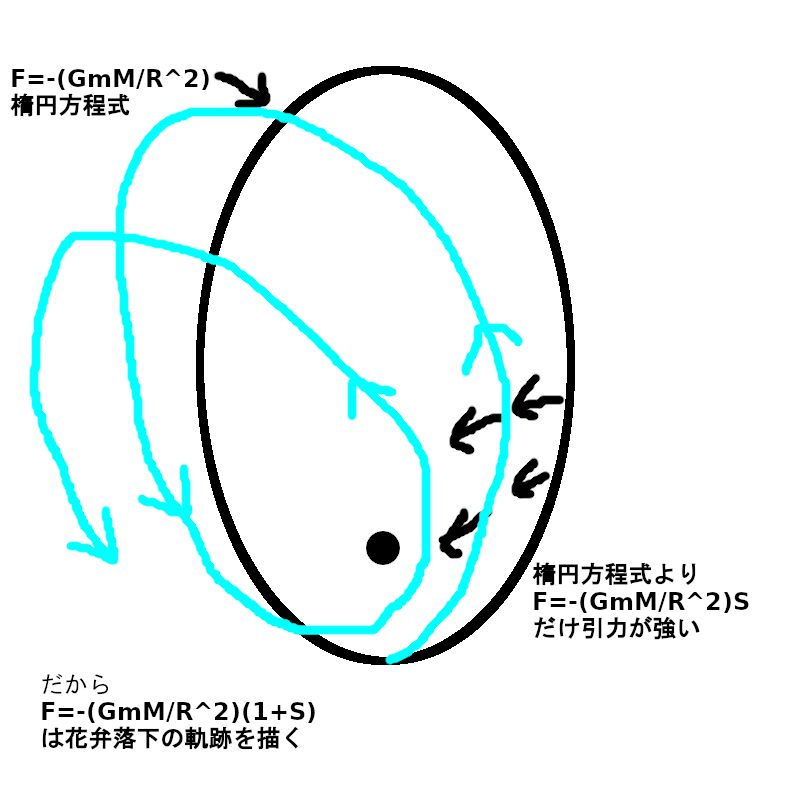
F=-(GmM/r^2)(1+S)が一般相対論の要請通りに
花びら落下の軌跡を描くことの図解
一般相対性理論の要請通りに重力波を放出して最終的には落下するという軌跡を描きます
ただし落下するには天文学的な周回が必要です
一般相対論の軌道の要請は
・花びら落下軌道
つまり
楕円軌道が進行方向に歪み徐々に高度を落としていく
というものです
相対論補正項をめちゃくちゃに大げさにした↓のシミュレートで
その要請を満たすことが確認できます
F=-(GmM/r^2)(1+S)の重力波を放出して軌道が不安定になるシミュレート
G=6.67e-11,m=1,M=100,r=1[AU]
ルンゲクッタ法で計算しているので不安定になるのは多分丸め誤差のせいじゃないです
S = × (v/c)^2
S = -0.5 × (v/c)^2:特殊相対性理論
S = 3.0 × (v/c)^2:一般相対性理論
S = 2.5 × (v/c)^2:一般相対性理論+特殊相対性理論
S = 0.0 × (v/c)^2:古典万有引力
F=-(GmM/r^2)(1+S)
S=(3.0/(1-e^2))(v/c)^2これを
S=(1e34/(1-e^2))(v/c)^2として
大げさに相対論補正項を設定して
その振る舞いを見る

ちゃんとこういう軌道になっています
#####################################################
(*A)の考察
近日点移動理論値
dφ=2π(3/2)(a/l)=2π(3/2)(a/((L/2)(1-e^2)))[rad/周]
dφ=360*3600(3/2)(a/((L/2)(1-e^2)))[秒/周]*[周/年]*[年]
1[AU]=149598700000[m]
太陽のシュバルツシルト半径a=2953[m]
水星軌道速度47872.5[m/s]
水星の離心率e=0.20563
水星の軌道長半径L/2=0.3871[AU]
水星4.15[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒/100年]
dφ'=360*3600*3*(v/c)^2*4.15*100=360*3600*3*(47872.5/299792458)^2*4.15*100=41.14[秒/100年]
ここで
41.14/42.9=0.959
1-e^2=0.958
だから
(3/(1-e^2))*(v/c)^2
だとすると
dφ'=42.9
になるから相対論補正項は
(3/(1-e^2))*(v/c)^2???
なぜならば一般の証明から
Sを調べます
3mu^2/(m/h^2)=3u^2h^2=3(1/r^2)(r^2dψ/ds)^2=3r^2((dt/ds)(dψ/dt))^2=3r^2(dψ/dt)^2(1/c^2)
=3(rdψ/dt)^2(1/c^2)=3(v/c)^2
と
ψは(*1C)よりr^2(dψ/ds)=h(定数)角運動量保存・・・(*3)
より離心率eがあるとき
(dψ/ds)^2=(h/r^2)^2=1/(1-e^2)
となる
注
楕円面積S=πa^2√(1-e^2)
dS/dt=h一定=S/T=πa^2√(1-e^2)/T
だから
(dψ/ds)^2=X/(1-e^2)
上へ戻る
確かめ算
近日点移動理論値
dφ=2π(3/2)(a/l)=2π(3/2)(a/((L/2)(1-e^2)))[rad/周]
dφ=360*3600(3/2)(a/((L/2)(1-e^2)))[秒/周]*[周/年]*[年]
dφ'=360*3600*(3.0/(1-e^2))(v/c)^2[秒/周]*[周/年]*[年]
1[AU]=149598700000[m]
太陽のシュバルツシルト半径a=2953[m]
水星軌道速度47872.5[m/s]
水星の離心率e=0.20563
水星の軌道長半径L/2=0.3871[AU]
水星4.15[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒/100年]
dφ'=360*3600*3*(v/c)^2*4.15*100=360*3600*3*(47872.5/299792458)^2*4.15*100=41.14[秒/100年]
1-e^2=0.958
41.14/0.958=42.9
金星軌道速度35020[m/s]
金星の離心率e=0.0068
金星の軌道長半径L/2=0.7233[AU]
金星1.633[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.7233)/(1-0.0068^2)*1.633*100=8.6[秒/100年]
dφ'=360*3600*3*(v/c)^2*1.66*100=360*3600*3*(35020/299792458)^2*1.66*100=8.6[秒/100年]
1-e^2=0.99995
8.6/0.99995=8.6
地球軌道速度297800[m/s]
地球の離心率e=0.0167
地球の軌道長半径L/2=1.0[AU]
地球1.0[周/年]
dφ=360*3600*3/2*2953/(149598700000*1.0)/(1-0.0167^2)*1.0*100=3.83[秒/100年]
dφ'=360*3600*3*(v/c)^2*1.0*100=360*3600*3*(297800/299792458)^2*1.0*100=3.83[秒/100年]
1-e^2=0.9997
3.83/0.9997=3.83
火星軌道速度24130[m/s]
火星の離心率e=0.0934
火星の軌道長半径L/2=1.5237[AU]
火星0.53[周/年]
dφ=360*3600*3/2*2953/(149598700000*1.5237)/(1-0.0934^2)*0.53*100=1.34[秒/100年]
dφ'=360*3600*3*(v/c)^2*0.53*100=360*3600*3*(24130/299792458)^2*0.53*100=1.33[秒/100年]
1-e^2=0.991
1.33/0.991=1.34
一般の証明#################################################
計量(c,i,j,k)のシュワルツシルト(球対称性を持つアインシュタイン方程式の真空解)の線素は
c光速度t座標時r動径座標θ余緯度座標φ経度座標2m=rsシュワルツシルト半径=2GM/c^2M質量
ds^2=(1-rs/r)c^2dt^2-dr^2/(1-rs/r)-r^2dθ^2-r^2sin^2θdψ^2
ds^2=(1-2m/r)c^2dt^2-dr^2/(1-2m/r)-r^2dθ^2-r^2sin^2θdψ^2・・・(*1)
その変分問題
δ∫((1-2m/r)c^2(dt/ds)^2-(dr/ds)^2/(1-2m/r)-r^2(dθ/ds)^2-r^2sin^2θ(dψ/ds)^2)ds=0・・・(*2)
各成分に対する方程式を導出すると
i=1,r,(*1)/ds^2
1=(1-2m/r)c^2(dt/ds)^2-(dr/ds)^2/(1-2m/r)-r^2(dθ/ds)^2-r^2sin^2θ(dψ/ds)^2・・・(*1A)
i=2,θ,
(d/ds)(r^2(dθ/ds))=r^2sinθcosθ(dψ/ds)^2・・・(*1B)
i=3,ψ,
(d/ds)(r^2sin^2θ(dψ/ds))=0・・・(*1C)
i=0,ct
(d/ds)((1-2m/r)(dt/ds))=0・・・(*1D)
成分を選んで
θはπ/2、dθ/ds=0、の赤道面上での話とし、θは定数なので(*1B)は無視する
ψは(*1C)よりr^2(dψ/ds)=h(定数)角運動量保存・・・(*3)
tは(*1D)より(1-2m/r)(dt/ds)=l(定数)エネルギー量保存・・・(*4)
(*1A)より
(1-2m/r)=(cl)^2-(dr/ds)^2-(h/r)^2(1-2m/r)・・・(*5)
rをψの関数として微分したものは
(d/dψ)(r(ψ))=r'=(dr/ds)(ds/dψ),(*3)より
(dr/ds)=r'(dψ/ds)=hr'/r^2,r=1/u,r'=-u'/u^2,(*5)より
(1-2mu)=(cl)^2-(hu')^2-(hu)^2(1-2mu)
u'^2=((cl)^2-1)/h^2+2mu/h^2-u^2+2mu^3・・・(*6)
ψで微分して
2u'u''=2mu'/h^2-2uu'+6mu^2u'・・・(*7)
u'=0,u=1/r(定数)という解は円軌道
u''+u=m/h^2+3mu^2・・・(*8)
この式はu''+u=m/h^2が万有引力の式に対応しイメージしてみると
シュワルツシルト時空の重力による加速度RelativeGravityの式は
r半径,G万有引力定数,M質量,V軌道速度,c光速度,S相対論補正項
Rg=-(GM/r^2)(1+S)
の形であるから、ここでh=r^2dψ/ds,m=kM/c^2,u=1/r,であって
相対論補正項3mu^2を検証すると、m/h^2でくくり
u''+u=(m/h^2)(1+3mu^2/(m/h^2)=(m/h^2)(1+S)の形にして、Sを調べます
3mu^2/(m/h^2)=3u^2h^2=3(1/r^2)(r^2dψ/ds)^2=3r^2((dt/ds)(dψ/dt))^2=3r^2(dψ/dt)^2(1/c^2)
=3(rdψ/dt)^2(1/c^2)
(rdψ/dt)は円の接線方向の速度だからそれを軌道速度Vとみれば3(V/c)^2と解けて
相対論補正項S=3(V/c)^2だから
ユークリッド幾何で
シュワルツシルト時空の重力による加速度RelativeGravityの式は
r半径,G万有引力定数,M質量,V軌道速度,c光速度,S相対論補正項
Rg=-(GM/r^2)(1+S)=-(GM/r^2)(1+3(V/c)^2)
と解ける
ただしこの説明は真円軌道の時
#####################################################
楕円軌道の証明
近日点移動理論値
dφ=2π(3/2)(a/l)=2π(3/2)(a/((L/2)(1-e^2)))[rad/周]
dφ=360*3600(3/2)(a/((L/2)(1-e^2)))[秒/周]*[周/年]*[年]
1[AU]=149598700000[m]
太陽のシュバルツシルト半径a=2953[m]
水星軌道速度47872.5[m/s]
水星の離心率e=0.20563
水星の軌道長半径L/2=0.3871[AU]
水星4.15[周/年]
dφ=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒/100年]
dφ'=360*3600*3*(v/c)^2*4.15*100=360*3600*3*(47872.5/299792458)^2*4.15*100=41.14[秒/100年]
ここで
41.14/42.9=0.959
1-e^2=0.958
だから
(3/(1-e^2))*(v/c)^2
だとすると
dφ'=42.9
になるから相対論補正項は
(3/(1-e^2))(v/c)^2となるか?
なぜならば一般の証明から
Sを調べます
3mu^2/(m/h^2)=3u^2h^2=3(1/r^2)(r^2dψ/ds)^2=3r^2((dt/ds)(dψ/dt))^2=3r^2(dψ/dt)^2(1/c^2)
=3(rdψ/dt)^2(1/c^2)=3(v/c)^2
と
メモ:軌道速度、真円、楕円
真円の扇の面積Aはr,θ,軌道速度vで
A=(1/2)r^2θ=(1/2)rv
v=2A/r
v^2=4A^2/r^2
また質量M万有引力定数Gで
v=√(GM/r)
v^2=GM/r
楕円の扇の面積Bはq,ψ,軌道速度wで
B=(1/2)q^2ψ√(1-e^2)=(1/2)qw√(1-e^2)
w=2B/q√(1-e^2)
w^2=4B^2/q^2(1-e^2)
また質量N万有引力定数Gで
w=√(GN(1+e^2+2ecosψ)/q(1-e^2))
w^2=GN(1+e^2+2ecosψ)/q(1-e^2)
3(v/c)^2のvを楕円軌道速度で適用しようとすると
(1+e^2+2ecosψ)が加味されているので
楕円軌道速度と真円軌道速度と
真円軌道で求めた3(v/c)^2で
あと足りない部分を補完して
(3/(1-e^2))(v/c)^2となる
これが一般相対性理論の楕円軌道の相対論補正項つまりカー解の答えとなる
したがって
楕円軌道(離心率e)の一般相対性理論を考慮した万有引力運動方程式は
F=-(GmM/R^2)(1+(3.0/(1-e^2))(V/C)^2)
と解けました
F力G万有引力定数mM質点質量R質点間距離e離心率V軌道速度C光速度
証明終了
#####################################################
古い説明
ψは(*1C)よりr^2(dψ/ds)=h(定数)角運動量保存・・・(*3)
より離心率eがあるとき
(dψ/ds)^2=(h/r^2)^2=1/(1-e^2)
となる
注
楕円面積S'=πa^2√(1-e^2)
dS'/dt=h一定=S'/T=πa^2√(1-e^2)/T
だから
(dψ/ds')^2=X一定/(1-e^2)
ここで
h=r^2dψ/ds'
だから
h^2=r^4(dψ/ds')^2
(dψ/ds')^2=h^2/r^4
これは
dS'/dt=h一定=S/T=πa^2√(1-e^2)/T
(ds'/dψ)^2^2=h^2/r^4(1-e^2)
=T^2/π^2a^4(1-e^2)
=(T^2/S'^2)
T/S'=1/h一定
S'=πr^2が真円なので
楕円成分は(1-e^2)にかかっているので結局
相対論補正項S=3mu^2/(m/h^2)=3(rdψ/dt)^2(1/c^2)=(3/(1-e^2))(v/c)^2
となりました
つまりやっぱり楕円面積S'=πr^2√(1-e^2)ってこと
だから注のまとめは
楕円面積S'=πa^2√(1-e^2)であり
相対論補正項S=3mu^2/(m/h^2)=3(rdψ/dt)^2(1/c^2)=3(v/c)^2
だと真円面積S'^2だから(1-e^2)で割った
相対論補正項S=3mu^2/(m/h^2)=3(rdψ/dt)^2(1/c^2)=(3/(1-e^2))(v/c)^2
が正しい楕円軌道の相対論補正項となる
したがって
楕円軌道(離心率e)の一般相対性理論を考慮した万有引力運動方程式は
F=-(GmM/R^2)(1+(3.0/(1-e^2))(V/C)^2)
と解けました
F力G万有引力定数mM質点質量R質点間距離e離心率V軌道速度C光速度
証明終了
#####################################################
このように
リーマン幾何の一般相対論を
ユークリッド幾何でおらは解いたのだが
アインシュタイン以来百年間誰も解けなかったことを
せっかく解いたのに
これでなんで
おらはノーベル物理学賞を貰えていないのだろう?
幻覚もまあ見るけれど数学はちゃんと出来るのに
なんでただの基地外扱いされんの?
あと社会の法律なんかよりも
万有引力の法則は強制力が全然強いはずですよん
反権力で反戦平和と愛を歌う
転がる石ころロックだぜい
万有引力は究極の不自由(仕事)の中の究極の自由(遊び)だ
この証明のようにおらには絶大な自信がたっぷりある
別にただ単に地球の
相対論的な万有引力の
運動の式ってだけ
もしも万有引力に逆らいたかったら
危ないから紐付けてバンジージャンプでもしてみてね
相対性理論的ケプラー方程式も解けるかもな
kepler=u+duでduの誤差をなくしていくんだけど
普通のケプラー方程式に
relkepler=u+du+ds^2=u+du+(3/(1-e^2)(v/c)^2)
これで良いのではないかな?
面積速度一定ってつまり
向心力(重力引力)一定と同じだし
面積差分の二乗つまり
U=ma^2ってことだ
ちょっと違うな
U=(1/2)mv^2+mgh
ポテンシャルエネルギー一定やろ
それで結局E=mc^2になるな
つまりここだ
i=0,ct
(d/ds)((1-2m/r)(dt/ds))=0・・・(*1D)
tは(*1D)より(1-2m/r)(dt/ds)=l(定数)エネルギー量保存・・・(*4)
ちょっと思いつき
dφ=360*3600(3/2)(a/((L/2)(1-e^2)))*4.15*100=360*3600*3/2*2953/(149598700000*0.3871)/(1-0.2056^2)*4.15*100=42.9[秒/100年]
dφ'=360*3600*(3/(1-e^2))*(v/c)^2*4.15*100=360*3600*(3/0.958)*(47872.5/299792458)^2*4.15*100=42.9[秒/100年]
だから
(3/2)(a/((L/2)(1-e^2)))=(3/(1-e^2))*(v/c)^2
(a/L)=(v/c)^2
実際に値を入れてみると
1[AU]=149598700000[m]
太陽のシュバルツシルト半径a=2953[m]
水星軌道速度47872.5[m/s]
水星の離心率e=0.20563
水星の軌道長半径L/2=0.3871[AU]
水星4.15[周/年]
(a/L)=(v/c)^2
(a/L)=2953/(0.3871*149598700000*2)=2.55e-8
(v/c)^2=(47872.5/299792458)^2=2.55e-8
ちゃんと出ました
この公式から色んなのが出来そう
だから例えば
楕円軌道(離心率e)の一般相対性理論を考慮した万有引力運動方程式は
F=-(GmM/R^2)(1+(3.0/(1-e^2))(V/C)^2)
と解けました
F力G万有引力定数mM質点質量R質点間距離e離心率V軌道速度C光速度
は
楕円軌道(離心率e)の一般相対性理論を考慮した万有引力運動方程式は
F=-(GmM/R^2)(1+(3.0/(1-e^2))(a/L))
と解けました
F力G万有引力定数mM質点質量R質点間距離e離心率a太陽のシュバルツシルト半径L衛星の軌道長直径
と等価です
離心率簡易計算
二質点P1P2においてP1の速度ベクトルV1としてその離心率eを簡易的に計算する
SP=P2-P1
θ=SPとV1のなす角
θ=0でe=1,θ=π/4でe=0だから
e=|cosθ|とする
θ=π/3,e=0.5くらいだし簡易計算ならまぁいいか違うけれど
上へ戻る
メモ:相対論的速度合成則
・xブーストの相対論的速度合成則
任意の方向にするには
まずx軸へ速度ベクトルを回転させ
xブーストし元に戻せばいい
Vx'=(Vx-V)/(1-(VxV/c^2))
Vy'=(Vy)/γ(1-(VxV/c^2))
Vz'=(Vz)/γ(1-(VxV/c^2))
逆変換は
Vx=(Vx'+V)/(1+(Vx'V/c^2))
Vy=(Vy')/γ(1+(Vx'V/c^2))
Vz=(Vz')/γ(1+(Vx'V/c^2))
■■■ 3Dプログラミング入門講座 ■■■
NAS6LIB
ポリゴンテスト解説・x3dom使い方
その1:ベクトル
その2:行列
その3:クォータニオン
その4:基本総復習・実践
その5:応用その1・メッシュアニメーション、動的テクスチャ
その6:応用その2・GLSL、カスタムシェーダー、キーボード、ファイル
その7:応用その3・ゲームプログラミング、タグの動的追加
その8:応用その4・GLSL、シェーダー、その2
その9:物理演算その1・電卓で相対性理論を解く方法
その10:物理演算その2・相対性理論的ニュートン力学
その11:物理演算その3・ケプラー方程式で惑星軌道シミュレーターを作る
その12:物理演算その4・ルンゲクッタ法で作った
相対性理論的ニュートン力学物理エンジンで惑星軌道シミュレーターを作る
その13:経路探索(A*:A-STAR)&巡回セールスマン問題 : 巨大サイズ : くろにゃんこ
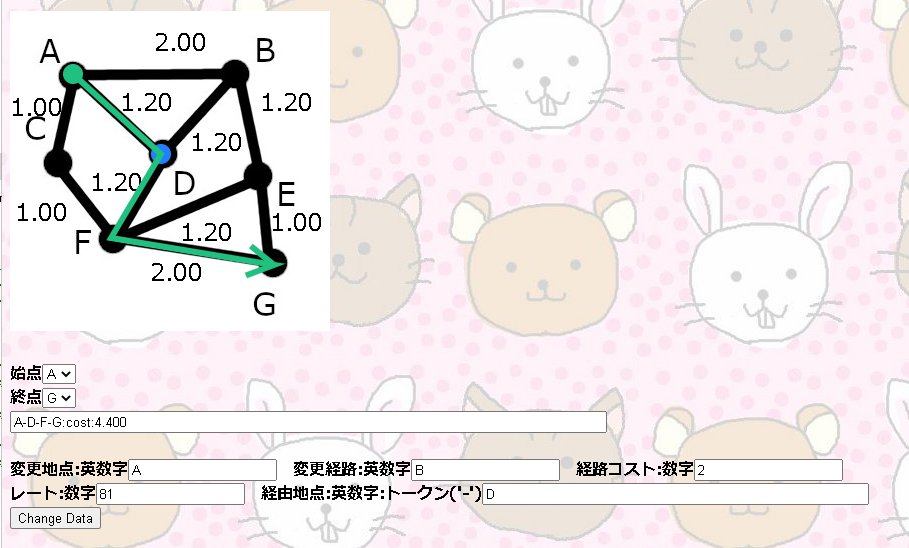
その14:プログラミングにおける配列テーブルテクニック
その15:javascriptのクラス活用法
その16:透視射影公式テスト
その17:ケプラー方程式カプセルライブラリ使用法
その18:CSVファイル処理
その19:物理演算その5・重力多体問題
その20:同次座標について(3D座標系の基本の基本)
その21:おさらいコモンクラスの宣言
その22:物理エンジンライブラリ解説(ケプラー方程式・ルンゲクッタ・相対論的万有引力)
■■■ THREE.JSプログラミング講座 ■■■
THREE.JSテスト解説・THREE.JS使い方
THREE.JS examplesをいじってみた(フレネル反射透過シェーダー)

THREE.JS (半透明シェーダー)
THREE.JS 3D演算で必要な計算(具体例)★とても重要★
THREE.JS THREE-VRM をいじってみた

<<prev GLSL、シェーダー、その2 : 相対性理論的ニュートン力学 next>>
戻る









