3Dプログラミング入門講座・その20:同次座標について(3D座標系の基本の基本)
同次座標は4次のベクトルと行列を用います
一般的なxyzwの順番ではなくNAS6ライブラリではwxyzの順番ですが計算結果は変わりません
ここではwxyzの順番で説明します
ベクトルVは
xyzは各軸ファクターでありwは同次(スケール)ファクターで出来れば1.0を保持します
ですのでV=(w/w, x/w, y/w, z/w)が同次の正規化です
行列Mは
○○|ww wx wy wz|
M=|xw xx xy xz|
○○|yw yx yy yz|
○○|zw zx zy zz|
であり
w行ベクトルは同次平行移動ベクトルです
Mの座標を意味します
xyz行ベクトルは各軸ベクトルです
Mの各軸の方向を意味します
尚Mの正規化(ノーマライズ)は
ax=√((xx/xw)^2+(xy/xw)^2+(xz/xw)^2)
ay=√((yx/yw)^2+(yy/yw)^2+(yz/yw)^2)
az=√((zx/zw)^2+(zy/xw)^2+(zz/xw)^2)
で
○○|ww/ww○wx/ww○wy/ww○wz/ww|
M=|xw/xw xx/xwax xy/xwax xz/xwax|
○○|yw/yw yx/yway yy/yway yz/yway|
○○|zw/zw zx/zwaz zy/zwaz xz/zwaz|
です
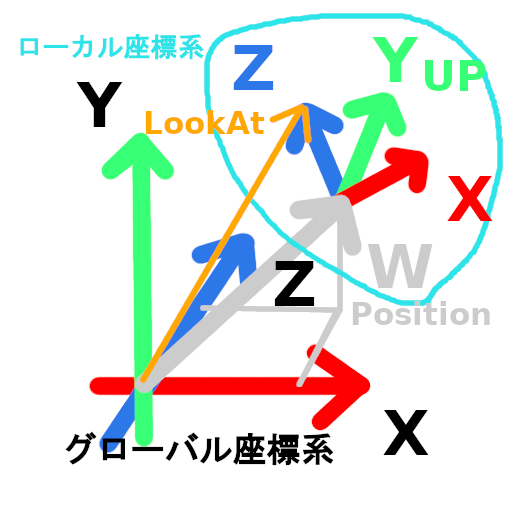
Mとはそれ自体で↑のようなローカル座標系を意味します
座標系Aに座標系Bとの積はA座標系の中のB座標系を意味します
threejsなどでカメラオブジェクトでは
matrixWorldInverseがカメラ座標系の逆行列ですが
それとは別に
カメラのPositionはカメラ座標系のW軸で
カメラのLookAtからPositionの差はカメラ座標系のZ軸で
カメラのUpはカメラ座標系のY軸で
そのZ軸とY軸の外積Z×Y=Xはカメラ座標系のX軸です
慎重を期すならば求めたZ軸とX軸との外積でY軸を求め更新して
XYZ各軸を鉛直関係にします
一応行列のノーマライズも忘れずに
以上でカメラのLookAtのローカル座標系が出来ました
ここら辺がわかると同次座標についての理解が深まると思います
あ、右手左手系でZ軸の向きが変わるのでZ軸が合うように適宜-1.0でもかけておいてください
■■■ 3Dプログラミング入門講座 ■■■
NAS6LIB
ポリゴンテスト解説・x3dom使い方
その1:ベクトル
その2:行列
その3:クォータニオン
その4:基本総復習・実践
その5:応用その1・メッシュアニメーション、動的テクスチャ
その6:応用その2・GLSL、カスタムシェーダー、キーボード、ファイル
その7:応用その3・ゲームプログラミング、タグの動的追加
その8:応用その4・GLSL、シェーダー、その2
その9:物理演算その1・電卓で相対性理論を解く方法
その10:物理演算その2・相対性理論的ニュートン力学
その11:物理演算その3・ケプラー方程式で惑星軌道シミュレーターを作る
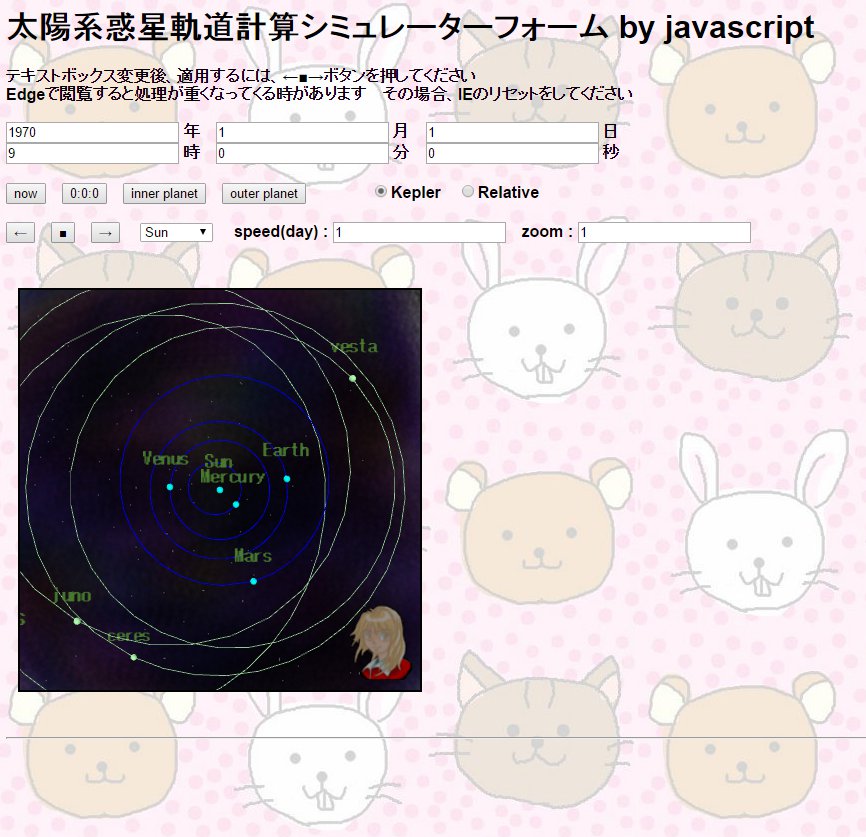
その12:物理演算その4・ルンゲクッタ法で作った
相対性理論的ニュートン力学物理エンジンで惑星軌道シミュレーターを作る
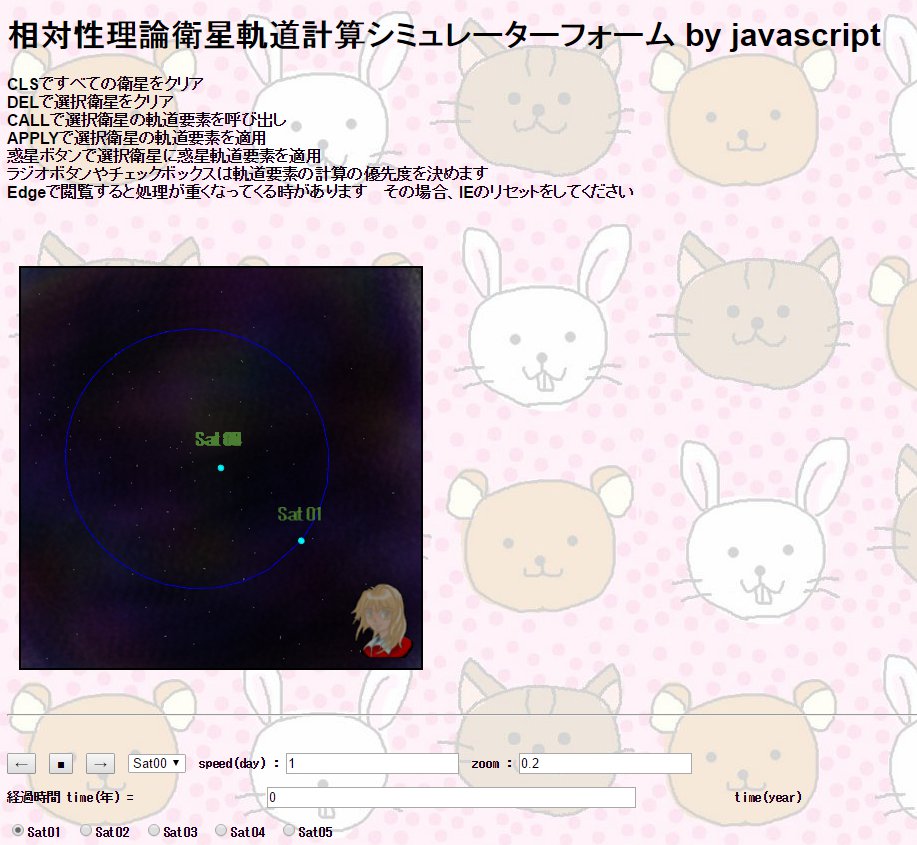
その13:経路探索(A*:A-STAR)&巡回セールスマン問題 : 巨大サイズ : くろにゃんこ
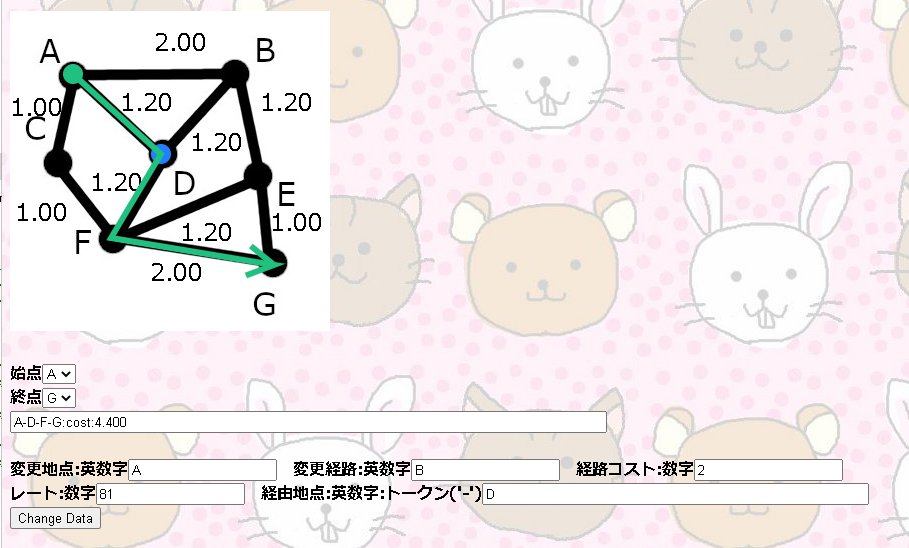
その14:プログラミングにおける配列テーブルテクニック
その15:javascriptのクラス活用法
その16:透視射影公式テスト
その17:ケプラー方程式カプセルライブラリ使用法
その18:CSVファイル処理
その19:物理演算その5・重力多体問題
その20:同次座標について(3D座標系の基本の基本)
その21:おさらいコモンクラスの宣言
その22:物理エンジンライブラリ解説(ケプラー方程式・ルンゲクッタ・相対論的万有引力)
■■■ THREE.JSプログラミング講座 ■■■
THREE.JSテスト解説・THREE.JS使い方
THREE.JS examplesをいじってみた(フレネル反射透過シェーダー)

THREE.JS (半透明シェーダー)
THREE.JS 3D演算で必要な計算(具体例)★とても重要★
THREE.JS THREE-VRM をいじってみた

<<prev 重力多体問題 : コモンクラスの宣言 next>>
戻る







