> ３Ｄプログラミング講座・その１６：透視射影公式テスト

３Ｄプログラミング講座・その１６：透視射影公式テスト







function enter(){
var canvas = document.getElementById('cnv');
 if (canvas.getContext) {
  var context = canvas.getContext('2d');
  context.fillStyle = 'rgb(0,0,0)';
  var sx = 600, sy = 600;
  context.fillRect(0,0,sx,sy);
  context.lineWidth = 3;
  context.strokeStyle = 'rgb(0,192,0)';
/*
透視射影公式
x=-(n/Pz)Px
y=-(n/Pz)Py
*/
  var n=1;
  var p = [[10,10,10],[-10,10,10],[-10,-10,10],[10,-10,10],[10,10,20],[-10,10,20],[-10,-10,20],[10,-10,20]];
  var pp = [];
  var zoom = 250;
//透視射影変換
  for(i = 0; i ＜ p.length; i++){
    pp[i] = [(n/p[i][2])*p[i][0], (n/p[i][2])*p[i][1]];
  }
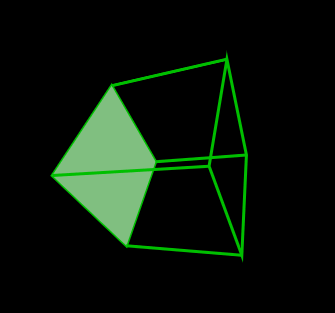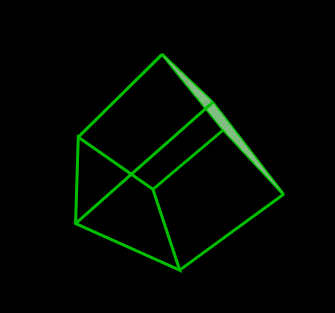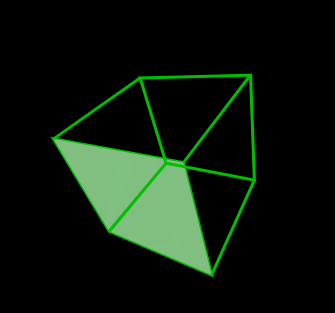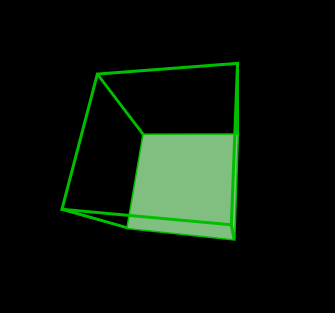
//ワイヤーフレーム表示
  context.beginPath()
  context.moveTo(pp[0][0] * zoom + sx / 2, pp[0][1] * zoom + sy / 2);
  for(i = 1; i ＜ 4; i++){
    context.lineTo(pp[i][0] * zoom + sx / 2, pp[i][1] * zoom + sy / 2);
  }
  context.lineTo(pp[0][0] * zoom + sx / 2, pp[0][1] * zoom + sy / 2);
  context.moveTo(pp[4][0] * zoom + sx / 2, pp[4][1] * zoom + sy / 2);
  for(i = 1; i ＜ 4; i++){
    context.lineTo(pp[i+4][0] * zoom + sx / 2, pp[i+4][1] * zoom + sy / 2);
  }
  context.lineTo(pp[4][0] * zoom + sx / 2, pp[4][1] * zoom + sy / 2);
  for(i = 0; i ＜ 4; i++){
    context.moveTo(pp[i][0] * zoom + sx / 2, pp[i][1] * zoom + sy / 2);
    context.lineTo(pp[i+4][0] * zoom + sx / 2, pp[i+4][1] * zoom + sy / 2);
  }
  context.closePath();
  context.stroke();
 }
}
簡単な透視射影のテスト

近平面への透視射影は
P' = [-(n/Pz)Px, -(n/Pz)Py]
なのでこれで点を変換して線をつなぐだけ


z = 10





実装方法その２

＜p＞z = ＜span id="count"＞10＜/span＞＜/p＞
＜canvas id='cnv2' name='cnv2' width='600' height='600'＞＜/canvas＞＜br＞
＜input type="button" id="BTN_DONE" name="BTN_DONE" value='Done' onclick="
var enter2 = () =＞ {
var cntelm = document.getElementById('count');
var zzz = Number(cntelm.innerText);
cntelm.innerText = Number(cntelm.innerText) + 10;
var canvas = document.getElementById('cnv2');
 if (canvas.getContext) {
  var context = canvas.getContext('2d');
  context.fillStyle = 'rgb(0,0,0)';
  var sx = 600, sy = 600;
  context.fillRect(0,0,sx,sy);
  context.lineWidth = 3;
  context.strokeStyle = 'rgb(0,192,0)';
  var n=1;
  var p = [[10,10,10],[-10,10,10],[-10,-10,10],[10,-10,10],
    [10,10,zzz],[-10,10,zzz],[-10,-10,zzz],[10,-10,zzz]];
  var pp = [];
  var zoom = 250;
  for(i = 0; i ＜ p.length; i++){
    pp[i] = [(n/p[i][2])*p[i][0], (n/p[i][2])*p[i][1]];
  }
  context.beginPath()
  context.moveTo(pp[0][0] * zoom + sx / 2, pp[0][1] * zoom + sy / 2);
  for(i = 1; i ＜ 4; i++){
    context.lineTo(pp[i][0] * zoom + sx / 2, pp[i][1] * zoom + sy / 2);
  }
  context.lineTo(pp[0][0] * zoom + sx / 2, pp[0][1] * zoom + sy / 2);
  context.moveTo(pp[4][0] * zoom + sx / 2, pp[4][1] * zoom + sy / 2);
  for(i = 1; i ＜ 4; i++){
    context.lineTo(pp[i+4][0] * zoom + sx / 2, pp[i+4][1] * zoom + sy / 2);
  }
  context.lineTo(pp[4][0] * zoom + sx / 2, pp[4][1] * zoom + sy / 2);
  for(i = 0; i ＜ 4; i++){
    context.moveTo(pp[i][0] * zoom + sx / 2, pp[i][1] * zoom + sy / 2);
    context.lineTo(pp[i+4][0] * zoom + sx / 2, pp[i+4][1] * zoom + sy / 2);
  }
  context.closePath();
  context.stroke();
 }
  return true;
};
var result = enter2();
"＞＜br＞





自力計算のワイヤーフレームの回転アニメーション

var TMan = new N6LTimerMan();  //タイマーマネージャー
var p=[];
var pp=[];
var time;
function GLoop(id) {
  time+=Math.PI/180;//1°のラジアン
  var i;
  var rp = [];
  pp = [];
//回転平行移動＆透視変換
  for(i = 0; i＜ p.length; i++) rp[i] = rot([0,0,1], 1 * time, p[i]);//z軸回り1°ずつ回転
  for(i = 0; i＜ rp.length; i++) rp[i] = rot([0,1,0], 2 * time, rp[i]);//y軸回り2°ずつ回転
  for(i = 0; i＜ rp.length; i++) rp[i] = rot([1,0,0], 3 * time, rp[i]);//x軸回り3°ずつ回転
  for(i = 0; i＜ rp.length; i++) rp[i][2] += 40;//z軸平行移動
  for(i = 0; i＜ rp.length; i++) pp[i] = frustum(1, rp[i]);//透視
//ワイヤーフレーム表示
var canvas = document.getElementById('cnv3');
 if (canvas.getContext) {
  var context = canvas.getContext('2d');
  context.fillStyle = 'rgb(0,0,0)';
  var sx = 600, sy = 600;
  context.fillRect(0,0,sx,sy);
  context.lineWidth = 3;
  context.fillStyle = 'rgb(128,192,128)';
  context.strokeStyle = 'rgb(0,192,0)';
  var zoom = 250;
  context.beginPath()
  context.moveTo(pp[4][0] * zoom + sx / 2, pp[4][1] * zoom + sy / 2);
  for(i = 1; i ＜ 4; i++){
    context.lineTo(pp[i+4][0] * zoom + sx / 2, pp[i+4][1] * zoom + sy / 2);
  }
  context.lineTo(pp[4][0] * zoom + sx / 2, pp[4][1] * zoom + sy / 2);
  context.closePath();
  context.stroke();
  context.fill();
  context.moveTo(pp[0][0] * zoom + sx / 2, pp[0][1] * zoom + sy / 2);
  for(i = 1; i ＜ 4; i++){
    context.lineTo(pp[i][0] * zoom + sx / 2, pp[i][1] * zoom + sy / 2);
  }
  context.lineTo(pp[0][0] * zoom + sx / 2, pp[0][1] * zoom + sy / 2);
  context.closePath();
  context.stroke();
  context.beginPath()
  context.beginPath()
  for(i = 0; i ＜ 4; i++){
    context.moveTo(pp[i][0] * zoom + sx / 2, pp[i][1] * zoom + sy / 2);
    context.lineTo(pp[i+4][0] * zoom + sx / 2, pp[i+4][1] * zoom + sy / 2);
  }
  context.closePath();
  context.stroke();
 } 
 TMan.timer[0].setalerm(function() { GLoop(0); }, 50);  //メインループセット
}
function rot(a,th,p) {
  var c = Math.cos(th),s = Math.sin(th);
  return [(c+a[0]*a[0]*(1-c))*p[0]+(a[0]*a[1]*(1-c)-a[2]*s)*p[1]+(a[0]*a[2]*(1-c)+a[1]*s)*p[2],
          (a[1]*a[0]*(1-c)+a[2]*s)*p[0]+(c+a[1]*a[1]*(1-c))*p[1]+(a[1]*a[2]*(1-c)-a[0]*s)*p[2],
          (a[2]*a[0]*(1-c)-a[1]*s)*p[0]+(a[2]*a[1]*(1-c)+a[0]*s)*p[1]+(c+a[2]*a[2]*(1-c))*p[2]];
}
function frustum(n,p) {
  return [(n/p[2])*p[0], (n/p[2])*p[1]];
}
function init() {
  p = [[10,10,10],[-10,10,10],[-10,-10,10],[10,-10,10],[10,10,-10],[-10,10,-10],[-10,-10,-10],[10,-10,-10]];
  time = 0;
}

function enter3() {
  init();
  TMan.add();
  TMan.timer[0].setalerm(function() { GLoop(0); }, 50);  //メインループセット
  return true;
}


要点
a軸th周りの回転公式
function rot(a,th,p) {
var c = Math.cos(th),s = Math.sin(th);
return [(c+a[0]*a[0]*(1-c))*p[0]+(a[0]*a[1]*(1-c)-a[2]*s)*p[1]+(a[0]*a[2]*(1-c)+a[1]*s)*p[2],
(a[1]*a[0]*(1-c)+a[2]*s)*p[0]+(c+a[1]*a[1]*(1-c))*p[1]+(a[1]*a[2]*(1-c)-a[0]*s)*p[2],
(a[2]*a[0]*(1-c)-a[1]*s)*p[0]+(a[2]*a[1]*(1-c)+a[0]*s)*p[1]+(c+a[2]*a[2]*(1-c))*p[2]];
}

near面透視射影公式
function frustum(n,p) {
return [(n/p[2])*p[0], (n/p[2])*p[1]];
}

エントリーポイント＆メインループセット
function enter3() {
init();
TMan.add();
TMan.timer[0].setalerm(function() { GLoop(0); }, 50); //メインループセット
return true;
}

メインループ
function GLoop(id) {

...

//回転平行移動＆透視変換
for(i = 0; i＜ p.length; i++) rp[i] = rot([0,0,1], 1 * time, p[i]);//z軸回り1°ずつ回転
for(i = 0; i＜ rp.length; i++) rp[i] = rot([0,1,0], 2 * time, rp[i]);//y軸回り2°ずつ回転
for(i = 0; i＜ rp.length; i++) rp[i] = rot([1,0,0], 3 * time, rp[i]);//x軸回り3°ずつ回転
for(i = 0; i＜ rp.length; i++) rp[i][2] += 40;//z軸平行移動
for(i = 0; i＜ rp.length; i++) pp[i] = frustum(1, rp[i]);//透視

...


　■■■　３Ｄプログラミング入門講座　■■■　
ＮＡＳ６ＬＩＢ
ポリゴンテスト解説・x3dom使い方
その１：ベクトル
その２：行列
その３：クォータニオン
その４：基本総復習・実践
その５：応用その１・メッシュアニメーション、動的テクスチャ
その６：応用その２・ＧＬＳＬ、カスタムシェーダー、キーボード、ファイル
その７：応用その３・ゲームプログラミング、タグの動的追加
その８：応用その４・ＧＬＳＬ、シェーダー、その２
その９：物理演算その１・電卓で相対性理論を解く方法
その１０：物理演算その２・相対性理論的ニュートン力学
その１１：物理演算その３・ケプラー方程式で惑星軌道シミュレーターを作る

その１２：物理演算その４・ルンゲクッタ法で作った 相対性理論的ニュートン力学物理エンジンで惑星軌道シミュレーターを作る

その１３：経路探索(A*：A-STAR)＆巡回セールスマン問題　：　巨大サイズ　：　くろにゃんこ

その１４：プログラミングにおける配列テーブルテクニック
その１５：javascriptのクラス活用法
その１６：透視射影公式テスト

その１７：ケプラー方程式カプセルライブラリ使用法
その１８：ＣＳＶファイル処理
その１９：物理演算その５・重力多体問題
その２０：同次座標について（３Ｄ座標系の基本の基本）


　■■■　THREE.JSプログラミング講座　■■■　
THREE.JSテスト解説・THREE.JS使い方
THREE.JS examplesをいじってみた(フレネル反射透過シェーダー)

THREE.JS (半透明シェーダー)

THREE.JS　３Ｄ演算で必要な計算(具体例)★とても重要★
THREE.JS　THREE-VRM　をいじってみた



＜＜　javascriptのクラス活用法　：　その１７：ケプラー方程式カプセルライブラリ使用法　＞＞


戻る